6_8_Mirror Correctors

EOS津野の
電子光学
講座

コンタクト: eostsuno@yahoo.co.jp

電子ミラーが軸対称な光学系であるにも拘らずなぜ負の収差を作ることが出来るかの説明として、シェルツァーの定理のなかに、電子の速度がその符号を変えた場合というと言う条件に当てはまるという説明がなされます。Roseのレビューにもそう書いてあります。しかし、この説明はミラーで負の収差が作れるのは間違いではないことを保障しているだけで、なぜミラーが負の収差を作るのかを説明してくれているわけではありません。ここでは、収差補正のときに必ず出てくる1936年のSchelzerの理論ではなく、電場分布、磁場分布を用いた説明と、光のレンズとミラーとの比較を基にした定性的な説明をしたいと思っています。

ミラー収差補正

ミラーによる負の色収差(Cc)生成の原理

　ミラーによる負の色収差(Cc)生成は定性的に理解しやすいものです。電子ビームが物面Zoから出てミラーのポテンシャルφが零となる位置で反射後、物面と同じ位置で像面ZiとなるZo=Ziを満たすようなポテンシャルUoとビームの角度αoを基準として考えることにします(図1参照)。これより大きなエネルギーのビームUo+Δは、ミラーのポテンシャルψ=0では反射できず、ψ<0まで潜り込みます。この結果、ビームはより強い力で偏向を受け、像面はZo よりミラーに近い側に来ます。エネルギーの強いビームが弱いビームより早くフォーカスしているので、色収差は負になります。物面、像面ともに実像の条件のもとに負の色収差が実現すると言うわけです。

エネルギーの高いビームとエネルギーの低いビームが、ミラーのある折り返し地点で次第にエネルギーを失って、ついには一旦止まってしまうわけです。その折り返しの場所はもとの電子のエネルギーによって違ってきます。電子は元々持っていた自分の電圧がゼロになるところで折り返してくるわけです。

そこで、上に書いたことをたとえ話で説明しますと、能力別の折り返し地点があるマラソンコースのようなものです。スピードの早い人は、折り返し地点が遠くにあり、スピードの遅い人はこれが手前にあるというハンディ付きのマラソン競争があるかどうか知りませんが、そんな場合に相当します。スピードの遅い人は早く折り返しますから、帰りのコースで前に出ます。スピードの早い人は遠くで折り返しますから、スピードの遅い人の後ろについてしまうわけです。これと同じことがミラーの中で起こって負の色収差として観測されるのです。

ミラーによる負の球面収差(Cs)生成の原理

球面収差とは、光軸から離れた電子ビームが受ける場の強さが中心軸付近で受ける場の強さよりも大きいために、軸から離れたビームほど強い収束作用を受けることによって生ずるものです(図2参照)。ザイデルの5収差と呼ばれている収差のすべてはこの理屈から説明されます。又、これは電場でも磁場でも同じです。このように球面収差はレンズ作用の元となっている電場や磁場が一様でないことにその原因があるのです。

電磁石の磁場の強さは、磁極から磁極へ向かう方向であるZ軸では、磁極表面の場が最も強く、磁極の中心に向かうにつれて弱くなります。一方、磁極の面に沿った方向、X,Yでは、ギャップ中心の磁場が最も強く、中心から離れるにつれて弱くなります。これは、Laplase方程式からの要請でZ方向の分布と、X,Y方向への分布はいつも逆になると言う関係があるからです。しかしながら、電子を通すためいったん穴を開けると、事情は一変します。もはや中心軸上で場は最大ではなくなります。なぜなら、穴のために磁極や電極は中心軸上には存在しないからです。場の強さは中心軸上でもっとも弱く、軸から離れるにつれて強くなります。こうしたレンズに電子ビームを通しますと、その中で電子の軌道は図2のようになるのです。中心軸付近を通るビームに対するレンズ作用は弱く、周辺を通るビームに対するレンズ作用が強くなるわけです。この状態が正の収差係数を持つ状態と定義されていますから、穴のないレンズが存在すれば、負の収差が作られるのではないかと想像されます。

両側のポールピースを穴なしにしたのでは電子ビームを入れたり出したり出来ませんので、いくら負の収差が作れるからと言って使い物になりません。しかし、片側が穴なしのポールピースを持つ電磁石ではどうでしょうか。実は片側だけ穴なしにしたレンズで負の球面収差を実現することは出来ます。片側だけの孔でも使える電子顕微鏡としては走査電子顕微鏡(SEM)や反射電子顕微鏡(LEEM)、光電子顕微鏡(PEEM)などいろいろありますので、これは有望かもしれません。しかし、残念ながら、負の収差を持つレンズは虚像しか作れませんでした。

シェルツァーの条件の最初に物面と像面が実像を作ると言うのがありました。もちろん、実像を作るレンズと組み合わせて、トータルで実像となるレンズにするという案もあります。しかし、全体として実像を作るレンズではトータルの収差が正になってしまいます。実像レンズの正の収差が虚像レンズの負の収差を上回るのです。

実は、ここでミラーの登場となります。なぜミラーだとレンズでは出来なかったことが出来るようになるのでしょうか。その説明には、光に対するガラスレンズやミラーと電子に対する金属製のレンズやミラーの比較をしてみるのがわかりやすいと思われます。

光のレンズと電子のレンズの違いはなんでしょうか。

光のレンズには、凸レンズも凹レンズもあります。しかし、電子レンズには凸レンズしかないと言われています。このため、電子顕微鏡の分解能は波長限界よりはるかに悪いと説明されてきました。それではなぜ電子に対するレンズでは凹レンズが作れないのでしょうか。この理由は、わかりやすく言えば、光のレンズは透明であるため光がレンズの中を通ることが出来るのに対し、鉄で作ってある電子レンズは電子に対して不透明なのでその通り道に穴を開けなければならないことによるのです。

多分、今まで聞いておられた理由は、軸対称レンズでは負の収差が作れないというシェルツァーの定理だったと思いますが、じゃあどうして軸対称だと負にならないのかがわかりませんでした。上の説明だと、わかったような気になるかと思いますが、実は同じことを言っているのです。

光と電子のミラーを比べてみると

電子の場合、物面と像面が実像の条件で負の球面収差は、レンズの場合には作れませんでしたが、ミラーでは作れます。レンズでは虚像になってしまう条件がミラーだと実像になるからです。光の場合は、レンズでもミラーでも負の収差が作れます。レンズの場合、レンズは光に対して透明だけれども電子に対しては透明でないため穴がいると言いました。そうしますと、鏡は光や電子を反射するもので、光や電子が反射するにあたって透明である必要もないし、穴もあけなくて良いことがわかります。つまり、ミラーは光と電子で共通なのです。電子は、ミラーに対して穴を開けなくてもよいので負の収差が実像で作れるのではないでしょうか。

このような光と電子に対するレンズとミラーの違いが収差補正の仕組みを考えるときのヒントになるのではないでしょうか。　負の収差が作れるかどうかについてはレンズでもミラーでも同じですが、負の収差を持ちながら実像を作ることが出来るのは軸対称な場ではミラーだけです。ただここで断っておかなければならないことは、電界ミラーでは、両電極に穴があいている場合でも負の収差を作ることが出来ることです。これは、負のポテンシャルを電極に与えることが出来ることによるもので、磁界よりも電界で自由度が高くなります。

ミラーのシミュレーション

　ミラーの中での軌道や収差の計算には二種類の方法があります。一つはハイパボリックミラーと呼ばれる形状(図5参照)を選択し、二段あるいは三段の電極について解析的に電場と軌道計算をする方法です。この方法は最初レンプラーによって計算され、実験も行われました。最近、パラボリックミラーとレンズの組み合わせのシミュレーションの論文が出ており、FEI社から収差補正PEEMも発表されています。

もう一つは、任意形状のミラーに付いて電場のシミュレーションを行う方法です。軌道計算は通常電子顕微鏡関係の軌道計算ソフトではZ位置に対する軌道の高さRを求めるのですが、ミラーでは電子がいったん止まって反対方向に進むため計算できません。そこで運動方程式に戻って時間に対する電子の位置を計算するソフトが作られていきました。もともと、市販の軌道計算ソフトでは、時間に対して電子軌道が計算されるソフトもあり、その場合はミラーが入っているからと言って特別な配慮は必要ないようです。電子の速度が遅くなるので、時間分割が細かくなりすぎて計算時間が長すぎるとか、データたーが多くなりすぎて表示が出来ないとかの問題が起こる程度で、時間設定を直してやれば解決します。

ドイツではSMARTプロジェクトが有名で、Cs, Ccの補正前後の実験結果も報告されています。アメリカでは PEEM3に付けられたミラーが良く知られています。これらの装置では同時に補正できるCsとCcの範囲が図で示されています。ミラーの形状や装置全体の構成も詳しく述べられています。

さて、実際に平面のミラーについて右側から左端にあるミラーに向かってビームを何本も出してやり、ミラーで反射したビームの軌道を調べた例を図7に示します。図にはミラーの電圧をある値にしたときの一個の場合しか示していませんが、この場合より少し電圧の絶対値を小さくしますと、ビームは反射せずにミラーにぶつかって消滅してしまいます。図の場合には、反射ビームは発散してしまっています。これよりミラー電圧の絶対値を大きくしますと、ますます軸から離れた方向に飛んでいきます。そこでわかったことは、平面のミラーでは、電子は発散するだけ、つまり、虚像を作る凹レンズの働きをするだけだと言うことです。文献に書いてあるミラーの図を見ますと、全てのミラーが凹んだ凹面鏡の形をしています。これは、飾りではなく、そうしないと実像が作れないからだったのです。
図8はミラーに曲率をつけた場合を示しています。上の図はミラーの形で、下の図はミラー近くの電子の軌道を切り出して示しています。入射ビーム全体の形は、図7と同じですが、反射ビームだけが違っています。反射ビームはほとんど入射ビームと同じ軌道を取って戻っていくようにミラーの電圧を調整してあります。下の図を見ると、反射する位置はミラーの直ぐ近くではなく、約4mm程度ミラーから離れた位置で反射しています。

ミラーの左側にある電極は、一番右側がアース電極で、真ん中の二本が電圧をかけてレンズ作用を行わせます。このミラーは収差補正器ですから、対物レンズなどの収差に応じてそれと同じ大きさで符号が反対となる収差を作らなければなりません。そのために、普通の電場レンズの電極を入れて、正の収差を作ってミラーが作る負の収差を調節するわけです。二枚の電極がある理由は、CsとCcの二つの補正をしなければなりませんから、自由度を二つにしているわけです。こうして、ミラーの曲率で大体の収差を補正すべきレンズの収差に合わせておいて、細かい調整は穴の明いた正の収差を作る電極によって行うと言うわけです。これがミラー補正器の原理になります。

ビームセパレータ

　電子ビームはミラーに対して垂直に入射し、反射ビームは垂直に跳ね返ってきます。このため、入射と反射のビームの軌道を分離するビームセパレータが必要となります。ミラーによる収差補正はビームセパレータが元々使われているLEEM用に最も多く利用されています。そして、ビームセパレータは元々使われていませんが、LEEMと同じ結像レンズ系が使われているPEEM(光電子顕微鏡)でも利用されています。　ビームセパレータは、オメガフィルタなどのインコラム型のイメージングエネルギーフィルタと同じ構造を持っていますから、必ずしも像の解像度や形状を損なうものではありません。しかし、収差補正後にはより大きな開き角でビームを使いますから、より収差の少ない措置が求められます。実際、収差補正付きオメガフィルタでは、大きな開き角出使いますと、フィルタの収差が目立つことが観測されています。ただし、ビームセパレータは分析装置と違い分散を必要としませんので、偏向角を小さくするなどの方法でそれ自身の作る収差を減らすことは出来ます。90°と言った大きな角度の偏向をさせるのではなく、60°や30度等に抑えた角度が使われる場合もあるのはそのためです。ハイパバリックミラーでは、偏向角を小さくする方法が取られています。

フィルタの収差のように二次収差が主たる収差になる場合は、二回フォーカスさせることによって二次収差のキャンセルをさせることが一般的です。しかし、オメガフィルタが360°ビームを偏向させる間にこれを行うのと比べ、ビームセパレータでは最大でも90°偏向の間に二回フォーカスさせることは困難です。この困難を克服するため、SMART , PEEM3 のいずれも二重構造の電磁石が用いられています。図9は二重構造のビームセパレーターのいろいろな使い方を示しています。また、図10では、片側の磁極とコイルのみを2D表示で示してあります。このビームセパレータで左側から入射したビームが真上で反射し、右側から出て行く様子をシミュレーションによって示したのが図11です。偏向角は二重コイル方式のビームセパレータでは、90°より大きくとることができます。その角度は内側と外側のコイルの電流比を変えることによっていろいろにとることができます。図11の場合には、平行入射したビームが中心付近でフォーカスして、再び平行ビームとなって出て行く様子が示されています。こうして、電子軌道の符号を途中で反転させることによって、二次収差のキャンセルが行われます。このためには、90°より大きな角度の偏向を行わせる必要があるわけです。

LEEMでもともと使うビームセパレータと収差補正で使うビームセパレータの二段で、収差のキャンセルを期待する場合もありますが、試料位置から出たビームの収差だけが加算されますから、もともとのビームセパレータはその半分しか収差が加算されません。収差補正のセパレータと合わせて、3/2個の領域が像の収差に寄与することになります。これは2個ではないので収差のキャンセル効果は期待できないのです。ビームセパレータを必要としないパルス型二段ミラー補正器も検討されています。二段のミラーでビームを折り返すのですが、ビームの入出射のためにパルスビームが必要となります。

このようにミラーによる収差補正ではビームセパレータの開発もミラーと同等の重要性を持っているのです。

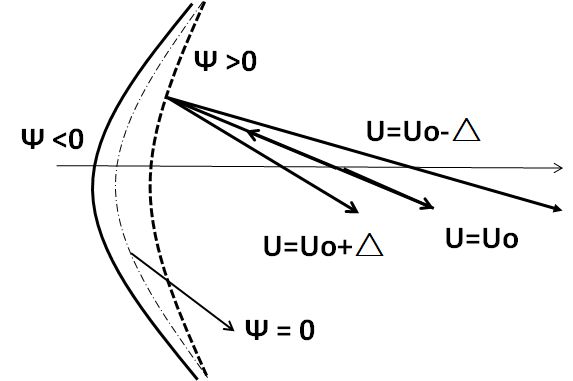図1.ミラーによる色収差補正の原理。

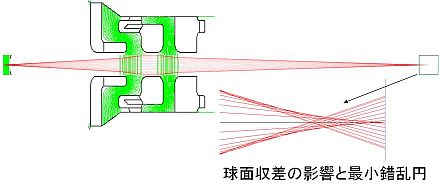図2.球面収差は角度の大きいビームが早く収束し、角度の小さいビーが遅く収束する。全角度範囲のビームを重ねたときに一番ビームの直径が小さくなる所を最小錯乱円と呼んでいる。

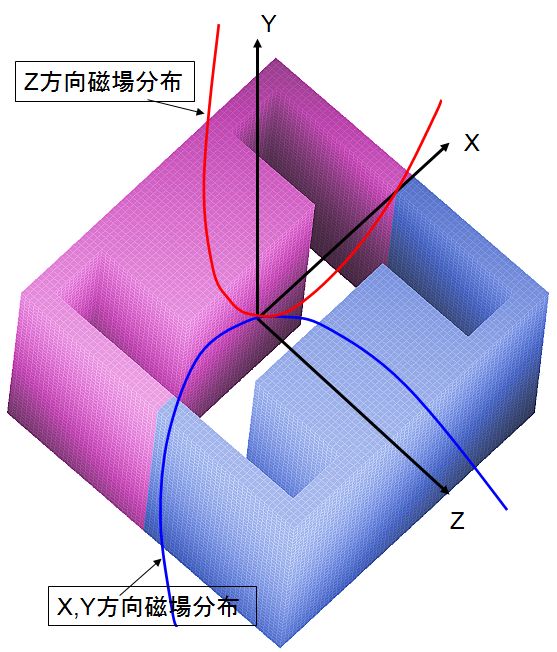図3.一般的な電磁石とその磁場分布。

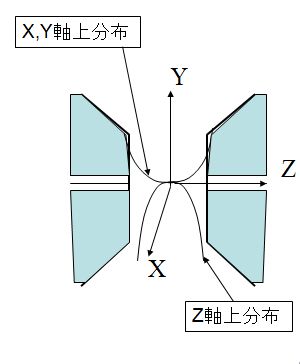図4.ビームを通すために孔を明けた電子レンズの磁場分布。

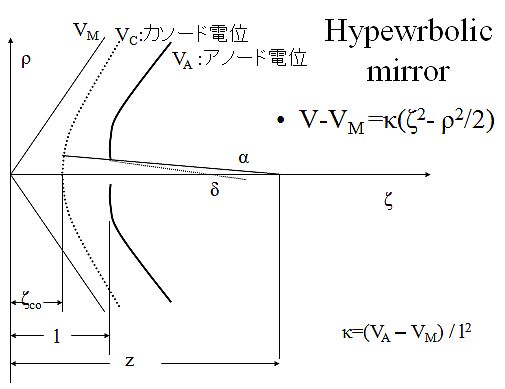図5.　ハイパボリック形状を表す式とその形状。

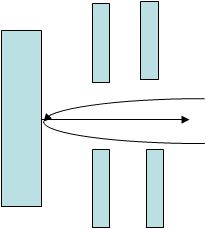図6. ミラーによる電子ビームの反射。

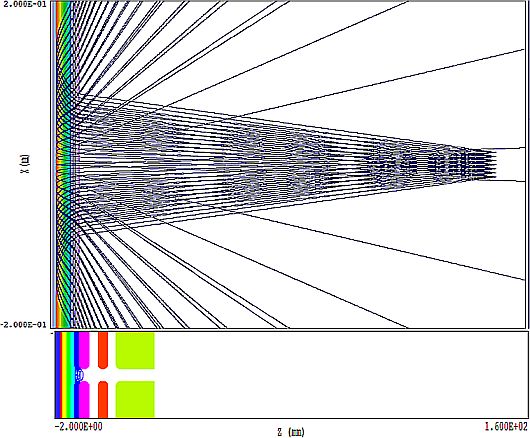図7. 平面ミラーでのビームの反射。

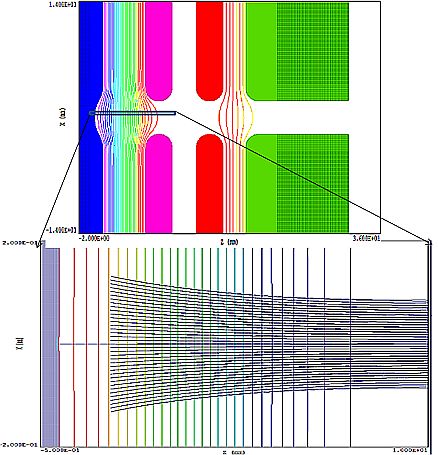図8. 曲面ミラーにするとビームは入射したときと同じ軌道を帰っていくようにミラー電圧を調節できる。

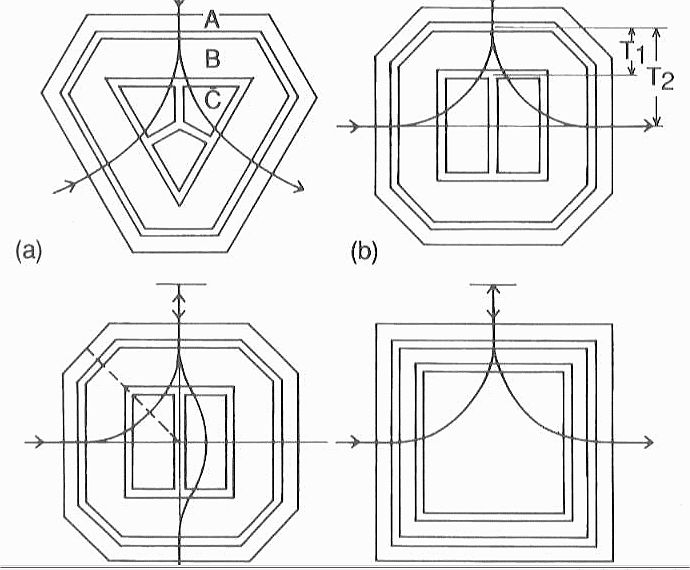図9.いろいろのビームセパレータ

図10.二段コイル式ビームセパレータ

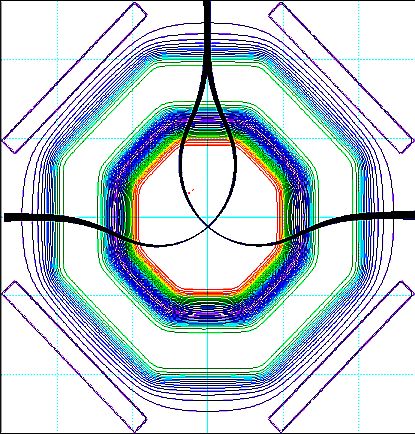図11.二段式ビームセパレータへの入射と反射ビームの軌道シミュレーション。

文献

A theoretical study of the hyperbolic electron mirror as a correcting element for spherical and chromatic aberration in electron optics
G. F. Rempfer
J. Appl. Phys. 67 (1990) 6027-6040.
Correction of chromatic aberration with an electron mirror
G. R. Rempfer, M. S. Mauck
Optik, 92 (1992) 3-8.

Image properties in an aberration-corrected photoemission electron microscope
R Konenkamp, T Jones, J Elstner, R Word, G Rempfer, T Dixon, L Almaraz, W Skoczylas
Physics Propedia 1 (2008) 505-511

SMART: a planned ultrahigh-resolution spectromicroscopefor BESSY II,
R. Fink, MR Weiss, E Umbach, D Prekszas, H Rose, R Spehr, P. Hartel, W. Engel, R. Degenhardte, R Wichtendahl, H Kuhlenbeck, W Erleback, K Ihmann, R Schlogl, H -J Freund, AM Bradshaw, G Lilienkamp, Th Schmidt, E Bauer, G Benner
J. electron Spec. Rel. Pheno. 84 (1997) 231-250.

Correction properties of electron mirrors
D. Preikszas, H. Rose
J. Electron Microsc. 1 (1997) 1-9.

Simulation of a mirror corrector for PEEM3
W. Wan, J. Feng, HA Padmore, DS Robin
Nucl. Instrum. Methods Phys. Res. A519 (2004) 222-229.

.EOS津野の事業内容