EOS津野の電子光学講座 コンタクト tsuno6@hotmail.com |
|
2. イメージングエネルギーアナライザの前夜
すべての電子光学機器内での電子の運動はニュートン・ローレンツの運動方程式 によって記述される。(d/dt)mv = -e(E + vxB) (1)
この式を一様磁場または次の式に従って変化する電場

の下で解くと、電子はこれらの場の中で円運動をする。ちなみに、ウィーンフィルタ の場合は一様電場と一様磁場のもとで円運動が打ち消しあって直進運動をする。 これらの場の中での運動方程式から時間を消去して電子の軌跡を表す軌道方程式 を求めることができる。軌道方程式は、電場、磁場、ウィーンの3種類のフィルタ に対して共通に次の式によって書き表すことができる。

これらの式の中のβx, βy, βdの値は、電場、磁場、ウィーンの各フィルタ に対して表Iのように書き表すことができる。

表I. 軌道方程式の係数
分散の係数βdは、電場で1, 磁場で-1/2となっているため、ウィーンフィルタ では両者の合計として1-1/2 = 1/2となり、偏向がキャンセルされてビームは 直進するが分散は磁場のそれが電場のそれの半分であるために残り、 エネルギーフィルタとして利用できる。
次にこの軌道方程式の解はマトリックスで表されるが、その中でx, y軸上の 解だけを求めると次の式で表される。
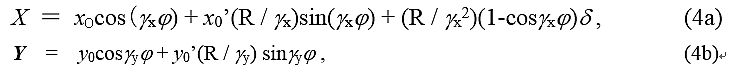
また、分散は次の式によって表される。

(5)式から、分散を大きくするためには回転半径を大きくするか、 回転角度を大きくとるしか方法がないことが分かる。ただし、δは加速電圧で 割ったエネルギー変動であるから、加速電圧を低くすることもエネルギー分解能 を高くする手段である。

表II. 軌道方程式の解の係数
表IIは、上に示した軌道方程式の解を一方向フォーカス(X方向のみにフォーカス) の場合と非点なし結像条件(x, y両方向に同時にフォーカス)のもとで解いた場合を 示している。
この他に、X, Y両方向で別の場所にフォーカスする二方向フォーカスの条件がある。
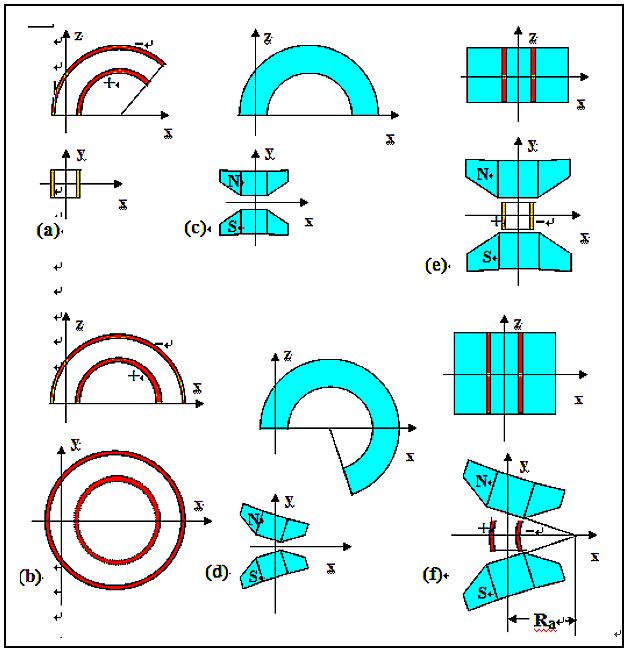 図1. いろいろのプリズム
図1. いろいろのプリズム図1は表IIIに基づいて描かれた各種フィルタであり、一方向のみにフォーカスする 場合と、非点なしフォーカスする条件でのフィルタを示している。
円筒電場と一様磁場では一方向にしかレンズ作用がないため、電場の場合は 球面電場、磁場の場合は傾斜磁極を用いることでy方向フォーカスを作り出している。 ただ、いずれの場合も4極場を作ってy方向フォーカスを実現しているため、それらの 場は同時にX方向には発散場を作ってしまうため、両方向にフォーカスを得るためには 回転角度が長く必要になっていることが分かる。ウィーンフィルタは基本的には 磁場フィルタと同じであるが、ビームが直進することと、磁極間隙に電極を挿入 する都合から磁極間ギャップが大きくとられている点に相違がある。
図1のすべての場合に、電子ビームの物面と像面は各フィルタの入り口と出口に 一致しておかれている。しかし、実験をする場合にこれは不便な条件である。 実験のためには物面も像面もフィルタから少し離れた位置に置くことができれば 便利である。すなわち、ドリフト空間を付け加えた場合にどう変わるかが次の 関心事である。
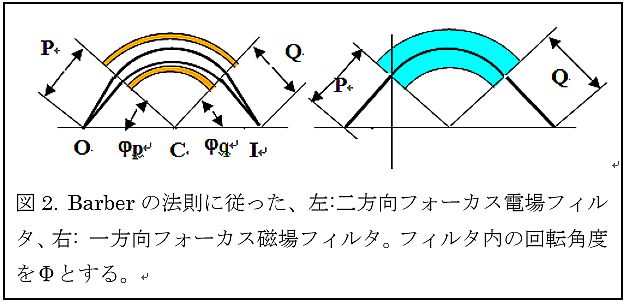 図2. バーバーの法則
図2. バーバーの法則図2はバーバーの法則として知られるもので、非点なしフォーカス電場フィルタと一方向 フォーカス磁場フィルタにおいては、ビームをフィルタ端面に垂直に入射させた場合、 フィルタ内でのビーム回転角とドリフト内での角度の合計の角度が180度になることが 知られている。つまり、物面と像面および回転中心の3点は必ず一直線上に並ぶという ものである。しかも、分散量はフィルタ内での回転角が小さくなっても、全角度 フィルタが占めていた場合と同じになることも知られている。つまり、物面位置に 電子源を置き、像面位置に検出器を置くために、フィルタの角度範囲を狭くしても 影響がないということになる。これはずいぶん有益な法則のように思えるが、 近年の半球フィルタの普及などをみると、全18°0の角度をフィルタが占めているもの がほとんどであり、また、磁場フィルタでは後で示すような端面傾斜が用いられている ことがほとんどであることから、バーバーの法則を利用したフィルタはあまり 見かけなくなった。
|
H3>目次(エネルギーアナライザ) .イメージングアナライザの前夜 .アナライザの分類 .飛行時間TOFの仕事関数測定 .飛行時間フィルターTOF2 .TOFと磁気ボトルの光電子分光 .CDA127 .SDA180(HDA) .半球アナライザ1 .半球アナライザ2 .キャスターン・ヘンリーフィルタ コンタクト・質問は、こちらまで ♪EOS津野"tsuno6@hotmail.com" |
目次(全体)1.最初のページ2.各種顕微鏡とそのレンズ設計 3.偏向と非点補正 4.光電子顕微鏡PEEM 5.エネルギー・アナライザ 6.Wien Filter 7.収差補正 8. スピン回転器 9.著者のページ 作成日 2012/09/25 修正 2018/03/04 . |