最初のイメージングエネルギーアナライザ:
1.キャスターン・ヘンリーフィルタ (プリズム・ミラー・プリズム)
電子顕微鏡に組み込まれたエネルギーフィルタはCastaingとHenryによって
1962に初めて作られた[1]。キャスターンはX-線分析装置EPMA(Electron Probe
Microanalysis)やイオン分析装置SIMS(Scanning Ion Microscope)の開発者
として知られ[2]、フランスのCameca社から多くの製品が発売されている。
電子顕微鏡の分析装置としてはここで説明するプリズム・ミラー・プリズム型
(PMP)のフィルタが知られているだけである。フランスではドイツに劣らず
電子やイオンの分析装置が盛んに研究されており、その理論的根拠は、
ドイツで作られた理論ではなく、フランス独自の1930年代に作られたCottの
理論が現代にいたるまで引用されている。PMPフィルタはその後Ottensmeyer
[3]によってフィルタの前段、後段に必要なレンズの組み合わせが明らかにされ、
ZeissのTEMに組み込まれて発売された。その装置は、生物用の
電子顕微鏡として大きく普及した。
このフィルタは、Prism-Mirror-Prismフィルタとも呼ばれているとおり、
二個の磁場型プリズムに電場ミラーが挟まれた構造をしている。図1では3角形に
描かれているのが二段のプリズムで、実際の電磁石もこのような3角形の磁極片
を持っている。現在からみると後で示す4個の磁石を組み合わせたオメガフィルタ
よりもずっと複雑で解析の困難さも大きいように感じられるが、このフィルタが
電場ミラーを使用していたためにその最初の開発当時は明らかにされていなかった、
対称性による二次幾何収差の消滅が自動的に実現され、電子顕微鏡像としての劣化なしに
エネルギー選択が行われたのである。
ビームはミラーを境に上下で対称な軌道を描いている。
エネルギーがずれたビームに関してはその対称性から外れた軌道を取っている。
1964年のHenryの学位論文[4]には実際のプリズムやミラーの写真も載っているが、
プリズムは模式図と同じような三角形をしていることが分かる。
もう一つ重要な点で、あとで説明するオメガフィルタと異なる点は、ミラーの前後で
分散が加算されていることである。分散が加算されているということは、収差も加算
されていることを意味している。しかし、分散が加算されるのは電子回折面である。
像も二回作られているが、第一の像面は、最初のプリズムの中ほどにあり、第二
の像面は第二のプリズムの中ほどにある。そこでは分散も二次収差も像面の前後で
キャンセルしあう関係にあり、最終的な像の中にそれらは現れてこない。つまり、
回折面、像面共に二回ずつ現れているが、回折面では分散が生じ、像面では二次
収差がキャンセルする。これに対し、次に説明するオメガフィルタでは、像面に
ついては同じであるが、二回目の回折面で分散がキャンセルするため、回折面を
三回作ることによって、分散を確保している。つまり、回折面は三回、像面は
二回のフォーカスとなっているのである。このように、キャスターン・ヘンリー
フィルタをベースにおいてオメガフィルタを見ることによって、両者の原理的な違いが
よく見えてくる。
2. オメガフィルタ (インコラムフィルタ)
2.1. オメガフィルタの歴史的背景
最初のオメガフィルタはPMPフィルタの静電ミラーをセクター磁石で
置き換える目的で始められた。それは、フランスのツールーズで計画
されていた超高圧電子顕微鏡に搭載するためである。もちろん、最初の
実験は超高圧電子顕微鏡で行われたわけではなく、100kVの普通のTEM
で制作された。Senoussi[5]によって作られたフィルタは図2に示すように
上下の中心に対して対称な形をしていない。このことが結局は、PMP
フィルタのように上下対称な軌道をフォーカスさせることによって
二次の幾何収差がキャンセルされることが明らかとなった。PMPフィルタでは
自動的に満たされていたため、特に認識されることのなかったことが、
オメガフィルタでは対称でない軌道を取ることも出来たことから、
収差キャンセルが実現せず、どうしてPMPフィルタのようにならないのか
を考えることで二次収差キャンセルの条件が明らかになったわけである。
その後、フランスではツールーズの超高圧電子顕微鏡にZanchi[6]の設計
になるオメガフィルタが搭載され、ドイツではRose[7]とWollnik[8]によって
二つの異なる型のフィルタが提案された。Roseの提案はその後弟子の
Lanio[9]によって設計されたフィルタがZeissより商品化[10]されLanioの分類
からA型、Wollnikの提案は、JEOL[11]によって商品化されB型と分類された。
Ωフィルタは最初と最後の磁石に対して途中の磁石の極性が反転し、
符号を含めたビームの全偏向角が零となるが、全磁石の極性を同一
として、偏向角の合計が360°となるαフィルタも1984年に提案されている[12]。
図3にアルファフィルタの一例を示す。アルファ型を横に引き延ばした
形のフィルタが日立によって商品化され、ガンマフィルタと命名された[13]。
2.2. オメガフィルタの基本光学系
Ωフィルタは、2つ(Senoussiのオメガフィルタ、α-フィルタ)、3つ(右側の
磁石をY-方向収束のために利用するため、2つに分割した場合)または4つの
セクター磁石によって構成されている。図4(a),(b)は、4つの磁石で構成され
るオメガフィルタを示している。電磁石は4個あるが、光学的には、3つの
レンズで構成されている。3つのレンズというのは、フィルタの
直前に前方のレンズによるクロスオーバーを形成し、フィルタ内で2つ、その
出口で3つ目のクロスオーバーを作り、そこにスリットが挿入されるから
である。この様子が図5(a)に示されている。なぜこのように3つもの
フォーカスを作らなければならないかという理由は、最初の
フォーカスで作られた分散が二つ目のフォーカスでキャンセル
してしまうため、もう一度フォーカスをさせて分散を作り直さ
なければならないからである。ただ、残念ながら、図5(a)では
ソフトウェアの不具合から、第二フォーカスで分散が加算され、
さらに第三フォーカスでも加算されるように描かれている。
なぜこのように分散を作ったり消したりしなければならないか
というと、それは、像面で分散と二次収差をキャンセルさせる
ことが最も重要だからである。
図5(b)に像面のフィルタ内での伝達の様子が示されている。この場合、
前段レンズの像面が第1マグネットに入ってから出来ている。これを中心面上
に結像し、二番目の像を第4マグネット上に作る。中心面に対して
軌道を対称に作る必要がある。クロスオーバーで見ると、3回のフォーカス
を行う系であり、拡大像で見ると、2回のフォーカスを行う系である。
キャスターン・ヘンリー型ではミラーでクロスオーバーが反転するため、
分散軌道は2回のフォーカスで加算されるため、軌道は単純であったが、
オメガフィルタでは分散軌道は奇数二次収差が回でなければならない。
二次の幾何収差をキャンセルさせるためには、像倍率を1倍にすることも重要である。
エネルギーフィルタを組み込んでいながら像には収差の影響が目立た
なくなる。幸い、電子顕微鏡の電子軌道には、像と電子回折という2つの
ビーム収束位置がある。分散を生じさせ、スリットでエネルギー範囲を選択
する操作は、この電子回折面を使うのである。
図5(a)では、フィルタの入り口に回折面を持って来ている。この回折面
の3回目のフォーカスをフィルタの出口に作るのである。分散は一回目
に作られるが、2回目では逆方向に作られるため、キャンセルしてゼロ
になる。再び3回目で作られた分散がフィルタの出口に形成される。
Ωフィルタは、イメージングのためのエネルギー
フィルタであって、エネルギースペクトルを取るだけのためには、四つもの
マグネットを持ち、三回もの結像をさせることは何の意味もない。
2.3.A-type オメガとB-typeオメガフィルタ
上では、クロスオーバーには分散を作るために奇数回のフォーカスが必要
であることを述べた。しかし、分散を生ずるのはX-方向即ち、磁極面と
平行な面だけである。これと垂直なY-方向即ち磁場方向には奇数回の
フォーカスは求められていない。この点に着目したのがWollnikで、
X-方向三回、Y-方向二回のフォーカスをさせるべきだということを
彼は主張した。X,Y方向でフォーカス回数が違う場合、像は裏返しになるが、
これは電子顕微鏡の場合特に問題にならないからである。図4(b)にはその
形状を図5(b)に軌道を示した。
Y-方向のクロスオーバーのフォーカス回数が二回に減少すれば、端面
傾斜角の減少が実現する。平行磁極面の電磁石では
X-方向フォーカスは出来るが、Y-方向にはフォーカス作用がない。
Y-方向フォーカスを実現するために、磁極の端面傾斜が行われているが、
この角度が45°を超えた場合急速に収差が大きくなることがわかっている。
Y-方向へのフォーカス回数が一回減れば、トータルとしての端面傾斜角度
が小さくて済む。これはΩフィルタの形状設計に大きなメリットになる。
実際、図4(a)と図4(b)を比較すると、端面傾斜角は図4(a)の方が大きく
なっていることがわかる。
B-typeの利点はわかったが、欠点はあるのか。本質的なことは
文献には出てこない。その理由は、収差補正にある。
A-typeは、収差補正が出来るが、B-typeは収差補正装置を組み込む
ことが出来ない。その理由は、A-typeでは、像軌道が中心面上でフォーカス
しているのに対して、B-typeではY-方向の像軌道が中心面でフォーカス
していないどころかここで最大値を持っていることである。
像軌道が中心面で光軸上にあれば、これに影響を与えることなく中心面に
収差補正用多極子を入れてクロスオーバー軌道を補正することが出来る。
このような補正はA-typeの場合にだけ行うことが出来る。
ただ、実際の応用上は、クロスオーバー軌道の収差を補正してもエネルギー分解能を
向上できるかどうかというくらいで、像に残った収差が補正されない。像軌道の収差を
補正するためには、クロスオーバー軌道がゼロになる面でなければならないが、そこは
スリット挿入位置と重なるため、困難が大きい。ということで、オメガフィルタは、
多極子補正にはA型であれ、B型であれ適していない。
収差補正多極子を組み込むのであれば電磁石を4子も使って
二次収差のキャンセルを行う必要はなく、電磁石は一個だけにして
多極子補正に収差の補正は任せればよいという考えもも成り立つ。
補正を前提とすれば、オメガフィルタの役割は、単に入射ビームと出射ビームの軸を
一致させてフィルタをレンズ系の途中に入れるインコラム型の
フィルタを実現するだけだとも言うことが出来る。
2.4.Ωフィルタの設計に要求される事柄
実際の設計に当たっては次のような点に注意が必要である。
1. 光軸が最初決まっていない。これは、偏向電磁石の形状と、
その励磁強度に依存する。
2. x,y方向によりレンズ作用が異なるが、最終的に非点の
ない像を作らなければならない。
3. クロスオーバー面でも非点のないフォーカスを作る
必要がある。
設計のプロセスとしては、まず、SCOFF(Sharp Cut Off
Fringing Field)近似によって、アナリティカルな解から
最適形状を決める。続いて、フリンジの影響を数値計算によって
求め、最終形状を決定する。
2. 5. 1. SCOFF近似
SCOFF近似では、磁場の強さはフィルタの縁で突然最大値になり、
反対側の縁で零に戻る。このため、マグネット内で磁場の強度
が一定となり、光軸はマグネット内では円弧をなし、マグネット
の外では直線となる。Paraxial軌道は、B1, B2に依存する。
ここで、ビームがマグネット端面に垂直に入射すると、B1
(一様磁場)だけで、B2(4極場)はかからない。磁極端面が
傾斜している場合には、4極場がかかるが、SCOFF近似の
ときは、この場は、傾斜角に比例する大きさで、δ関数
で与えられる。
一方、2次収差は、B1,B2,B3に依存する。SCOFF近似では、
B3はマグネットの端面でのみ発生し、やはりδ関数で
与えられる。B3の大きさは端面傾斜角と、端面が直線
ではなく曲面になっている場合はその曲率によって決まる。
収差は、場のある区間に渡っての積分で与えられるが、
SCOFFでは、場がδ関数で与えられるので、解析的な関数
として求めることが出来、Roseの論文に記載されている。
このようにして、SCOFFの場合には、収差は解析関数で
求められ、収差積分を数値的に実行する必要がない。
2. 5. 2. SCOFF下でのΩフィルタの設計
Ωフィルタは中心面対称を成しているので、解析は、中心面
から後半部分だけに限ることが出来る。SCOFFの下では、解析
に当たってのパラメータは次のとおりである。
マグネットの半径 R3, R4
ビーム偏向角度 Φ
ドリフト長 L3 (対称面からマグネット3まで), L4
(マグネット3とマグネット4の距離)、L5 (マグネット4から
スリット面までの距離)及びLL(最終像面とスリット面の距離)、
マグネット端面の傾斜角 τ1, τ2, τ3, τ4
ΩフィルタのタイプによるX,Y方向のフォーカス回数の別。
A-type(X-3, Y-3), B-type(X-3, Y-2)
これらの値の初期値を決めてビームを基本となる4軌道に
ついて飛ばしてみる。通常、フォーカスを得ることが出来ない
ので、端面傾斜角を変更し、フォーカスが得られる条件を探す。
うまく見つからない場合には、さらにドリフト長を変化させる。
フォーカスが得られれば、分散の大きさと2次収差の計算が
実行できる。
このように光軸が曲がった系では、ラウンドレンズの場合
とまったく異なる重要な事実がある。それは、フォーカス
は設計で決まるということである。ラウンドレンズの場合は、
フォーカスは電圧やアンペアターンの調整によって合わせる
ことが出来る。しかし、曲がった光軸を持つ系では、
フォーカスは光学系の形状で与えられるので、後で変更する
ことが出来ない。それではアンペアターンは何を決めるかといえば、
それは曲率半径である。フォーカス合わせのためにアンペア
ターンを変えてしまうと、ビームは光軸から外れてどこかへ
行ってしまう。このように、曲がった光軸系では、フォーカス
の精度がシミュレーションの誤差で決まってしまうので、
シミュレーションの重要性が非常に高くなることがわかる。
2.6.フリンジの磁場分布を使った軌道計算と収差の積分
SCOFFによる設計は、大体の見通しを与えるだけで、実際に製作
する磁石等の形状や配置を決めることは出来ない。フリンジ場
の下では、光軸すらもSCOFFの円軌道と異なっている。
フリンジ場では磁場の強さが場所によって変化しているので、
そこを通る電子ビーム軌道の回転半径は刻々と変化する。そこで、
本当の光軸を求めることは絶望的に難しい作業となる。ここでは、
本当の光軸の入り口と出口を求め、これらがSCOFFの光軸と一致する
ように調整するという手法を用いることにする。これは、虚像の
レンズの場合に、次のレンズから見て像はどこにいたことにすれば
良いかを決めること同じで、実際の像については考える必要がなくなる。
フリンジ場は、図6のような分布を持っている。そこで、フィルタの
領域を次の3つに分けて考える。まず、1. 磁場のないドリフト領域、
2. 磁場の変化しているフリンジ領域、3. 磁場が一定値を持つマグネット
内部領域。3の領域内では、場は一様で分布を持たないと考える。実際には
マグネットのポールピーの幅によって、場の強さは分布を持つが、この分布
を無視して一様場を仮定する。次に、2のフリンジ領域では、フリンジ場の
分布は端面傾斜角、あるいは曲面によらず一定であると考える。こうすると、
フリンジ場の分布は、マグネットのギャップ長Sと、ミラープレートと
マグネットの距離Gの2つだけに依存することになる。この2次元的分布を
別にシミュレーションによって求めておく。必要とあればミラープレート
のギャップがマグネットのギャップ長と異なる場合も考慮できる。この
仮定では、3次元的分布は考慮しないので、ポールピース面が傾斜して
いる場合には対応できない。しかしながら、これまでの経験則として
磁極面傾斜を持つ場合には分散を大きく取れるという利点があり、端面が
曲率を持つ場合には収差が提言されるという利点があるものの、いずれの
場合も実験的な成功を収めているケースがほとんどないことから、
それらの場合が考慮できない仮定をしてもかまわないともいえる。
これら2つの場合が実験的にうまくいかないケースが多い理由としては、
偏向磁石が1個ではなく何個かの組み合わせで用いられていることに
よるものと考えられる。磁石が一個だけで使われる場合には両者とも
成功裏に使われているケースが見られるからである。
ポールピース面が傾斜している場合を扱う方法は、ポールピースの
ある傾斜角に対して、端面傾斜を例えば10°おきなどの飛び飛びの
値にしたときの3次元磁場分布をあらかじめ求めておき、これを
テーブルデータとして記憶しておく。次に、フォーカスの操作を行って、
端面傾斜角がある値になった場合に、そのときのフリンジ場の分布
を先のテーブルから内挿によって求め、起動を計算することになる。
さて、実際の光軸はSCOFFの光軸とはずれる。
このずれをドリフト長の調整によってSCOFFに一致させる。全体の
軌道をSCOFFに一致させることは出来ないが、3番目のマグネットの
入り口と、4番目のマグネットの出口における光軸をSCOFFと一致する
ように、フリンジ場の分布の中心位置の座標をシフトさせて、光軸を
計算し、この出口がSCOFF軸と一致するまで試行錯誤的にフリンジ場の
位置をア調整する。
次に軌道と収差を求めるためには、ビームの各点でのB1, B2, B3の
値を求めなければならない。磁極端面の傾斜があるので、磁場の
X成分と、Y成分がこの傾斜角θによって決まる。次にフリンジ
磁場分布B(ζ)の一回、2回微分を求めておく。これらを用いて
光軸上の各点での磁場の多極子成分が計算される。
これらの場の値を使って、paraxial方程式をRunge-Kutta方程式
で求める。このとき、4つの軌道方程式のフォーカスを合わせな
ければならない。像軌道Xα, Yβは像面にフォーカスさせなけ
ればならないし、 クロスオーバー軌道Xγ, Yδはクロスオーバー
(スリット面)にフォーカスさせる必要がある。これらの4つの
フォーカスは、基本的にはマグネットの4つの端面傾斜角を変化
させることによって合わせることが出来るが、これらの端面傾斜
角のどれかが、大きすぎる場合には、ドリフト長の長さを変えて
フォーカスを合わせるようにする。
3. セクター磁石と多極補正子
- Krivanekのアウトオブコラムフィルター-
.1. パラレル検出型磁場プリズム
Krivanekらが電子顕微鏡の像観察室の下に取り付ける(アウトオブコラム
方式)のエネルギーアナライザを発表したのは京都で1986年に開かれた
国際電子顕微鏡学会でのことである[14]。
このフィルタは、TEMの投影レンズのクロスオーバーをエネルギー選択
スリットにフォーカスするにあたって、セクター磁石の形状だけでは
うまくいかない場合に備えて、4極子が使われている。フィルタの前段
にあるのはは6極子で、収差の補正ができる機能を持っているが
あくまでも補助的なものと考えられる。セクター磁石は端面が傾斜
しているばかりではなく、曲面にもなっており、二次収差の補正も考慮
されている。フィルタ後方の4極子は、非分散面(Y)と分散面(X)
とで異なっている。まず磁場プリズムによって作られるフォーカスは
Y方向ではQ1レンズ上、X方向ではQ2とQ3の間に来るように設定されて
いる。これは磁場プリズムの端面角度の調節に置いて機械的に行われた
ものであるというか、たまたま作った磁場プリズムのフォーカス位置
がそのようにずれていたということだと考えられる。磁場プリズムの
分散量は、加速電圧が100kVということもあって、わずか数mm/eVと
小さいため、ここで用いられたParallel検出器の空間分解能である
50μm/eVに到底及ばない。このため、X方向の分散を拡大しなければ
エネルギー分布を観測することが出来ない。ただ、Y方向に関しては、
検出器である光ダイオードアレイの幅である2.5mmより少しだけ小さい
大きさにすれば検出器を有効に使うことが出来る。
このような前提で3枚の4極子レンズが使われる。メインの拡大は、
二番目のQ2レンズによって行われる。Q2レンズはX-方向では発散、
Y-方向では収束レンズとして作用する。Y-方向では、Q2の収束
レンズのフォーカスがQ3レンズ上に来るように設定されているので、
Q3レンズの調節ではX-方向のみの付加的なフォーカス調整を行うこと
が出来る。
Q1レンズはY-方向には作用しないようにここでフォーカスが作られて
いるので、X-方向の軌道がうまくQ2レンズに入射できるように調節する
ことが出来る。このように、いくつもの4極子レンズがあるため、一見
複雑な調整が必要なように見えるが、各レンズの役割がしっかり決められ
ており、その調節が一つの役割だけを果たすことが出来るようにうまく
設計されている。文献では、Q1はスペクトルのフォーカスを助け、Q3は
Q2の強拡大による収差を軽減するための調節として使われると記載されている。
5.2. イメージングエネルギーフィルタ
1990年代から2000年代にかけて、キャスターンヘンリー型やオメガ型
のインコラム型のフィルタの普及に伴い、アウトオブコラム型の
フィルタもイメージングエネルギーフィルタとして使えるようにする
必要から、セクター磁石はそのままで、6個の4極子と5個の6極補正子を持つ
イメージングエネルギーフィルタが発表された[15]。
クロスオーバー軌道はスリット上に投影レンズからのクロスオーバーを
フォーカスさせ、ここに展開したエネルギー分散の一部をスリットに
よって選択するためのものである。一方、イメージ軌道は電子顕微鏡像
をまずはフィルタの中央付近で一度像にし、それを再び検出器上に投影
するのであるが、ここで、クロスオーバー上に展開した分散を消滅させ、
さらにフィルタによって導入された二次収差を6極補正子によってキャンセル
しなければならない。4極子はこの6極子による収差キャンセルをどこで
何に対して行うかを決めるために使われている。4極子によって、
X-軌道とY-軌道でほぼ平行四辺形が作られている。X-軌道の
高さが高くなったところで、Y-軌道は軸をよぎっており、逆も成り立っ
ている。この基本軌道は4-8極子による球面収差補正と同じ
原理で行われているものと考えられる。球面収差は三次の収差であり、
8極子によって補正されるが、フィルタの作る収差は二次収差なので、
6極子によって補正される。X-方向の収差を補正する場合にはY-方向の軌道が
軸をよぎっており、6極補正子はY-方向には影響しない。ただ、二次収差は
数が多く、球面収差の補正のように、4個の開口収差のみを補正すればよい
場合と異なるため、4極子が作る基本軌道も複雑な形をしている。
磁場プリズムの形を見ると、端面が曲面をしていることから、設計的には
二次収差をキャンセルしているものと思われるので、6極子の役割は、
設計値からのずれの分の補正で済んでいるものと思われる。この点が
Castaing-Henry フィルタやΩフィルタと異なる点で、これらの対称性
によって二次収差をキャンセルする方式のフィルタでは、フィルタに対する
ビームの入り方によって収差が出たりうまく消去されたりするため、
ビームの調整に長い時間を要することになる。一見すると、10個以上もの
多極補正子を持つフィルタの方が調整に要する手間が大きいように思ったが、
現実の装置の普及の違いが、むしろ多極子補正方式の方が使い易かったことを
実証している。
7 まとめ
ここではTEMに接続して用いられるイメージングエネルギーフィルタを取り上げ、
単純にエネルギースペクトルを取れば良いアナライザからエネルギー選択をした
イメージングを行わせるためには何が必要かを見てきた。その最初は二つの
磁場プリズムとその間に電場ミラーを挟んだPMPフィルタであった。この
フィルタでは、磁場プリズムが作り出す二次収差を対称な二つのプリズムを
用いることによってキャンセルさせていた。しかし、二次収差がこのような
対称な二つのプリズムでキャンセルされるということに対する認識がなかった
。加速電圧を高くするために、電場ミラーを別の磁場プリズムで置き換
えたところ、対称性が自動的には満足されなくなり、大きな二次収差が出て
しまった。そこで、対称条件の重要性が認識され、オメガフィルタやアル
ファフィルタといった対称条件を満足するイメージングフィルタが開発された。
これに対して、あくまでも一個の磁場セクター磁石を使い、二次収差は4-6極補正子
によってキャンセルしようというフィルタが現れた。球面収差補正が当たり前の
ように使われる現在の状況下では、対称条件によって自動的に
二次収差をキャンセルする方式は、フィルタが完成した後で設計と現実の装置
との狂いによって残る二次収差の影響が、球面収差補正によって、はじめて
使えるようになった大きなビーム入射角の下であらわに見えるようになった。
結局は二次収差補正機能を持っている4-6極補正子付フィルタに性能的に及ば
ない結果となっている。イメージングフィルタ開発の当初は、自動的に補正
できるフィルタの方が、補正子を使う方式より優れていると思われたが、結局、
設計時には完全には補正できるぃるたを見通すことが出来ず、実験時に補正
しなければならないということになれば、大掛かりな対称条件を入れるよりも、
最初から補正子に頼る方が優れていることになり、これも時代の流れと考える
ほかはない。
|
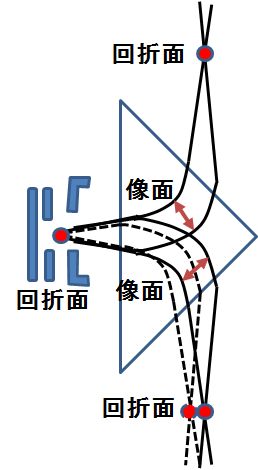図1. キャスターン・ヘンリーフィルタの概略。
| 
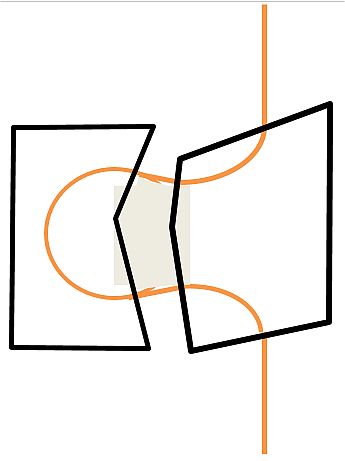図2. Senoussiによって最初に実験されたオメガフィルタ。 |
図3. 合計の回転角が360となるアルファ・フィルタの形状。 |
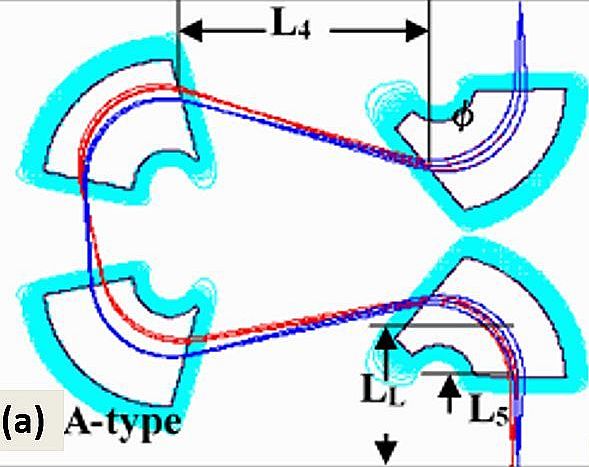図4(a). Omega Filter A-typeの形状。 |
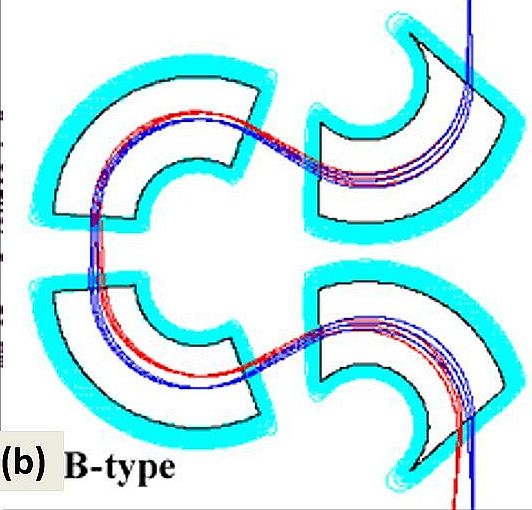図4(b). Omega Filter B-typeの形状。 |
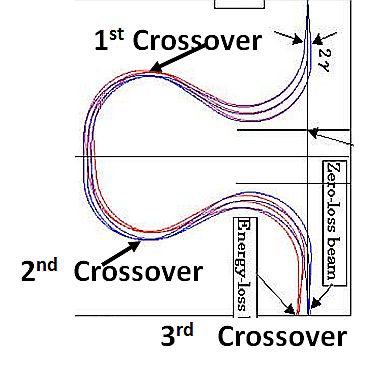図5(a). Omega Filter A-typeクロスオーバー軌道。
| 
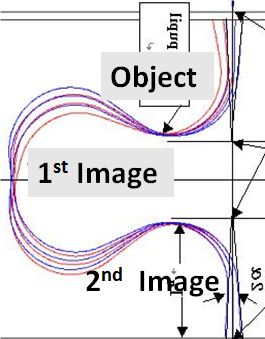図5(b). Omega Filter A-typeイメージ軌道。
| 
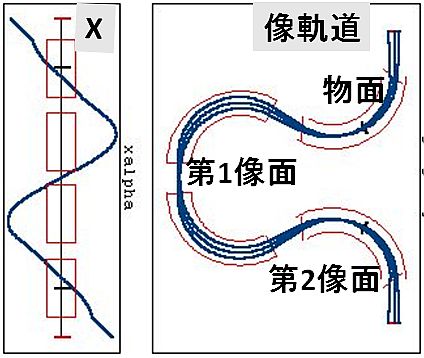図6(a). Omega Filter B-typeの像軌道のX方向。
| 
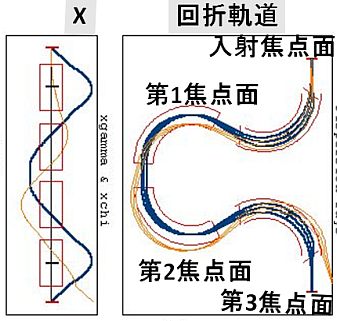図6(b). Omega Filter B-typeの回折軌道のX方向。
| 
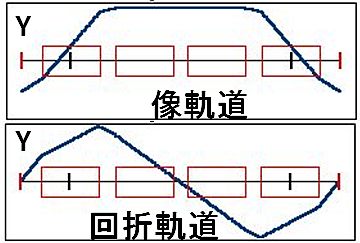図6(c). Omega Filter B-typeの像・回折軌道のY方向。
| 
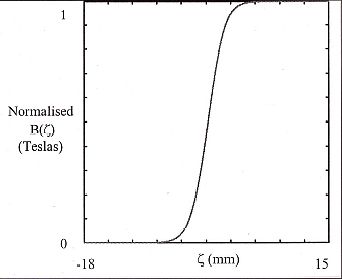図7. Omega Filter フリンジ場の分布。
| 
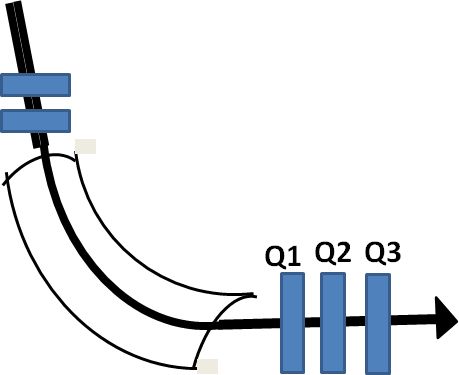図8. セクター磁石と4極子補正による非点なし結像EELS。
|
References
[1]. Focusing of Charged Particles, vol 2 (1967) Academic Press, New York,
Chapter 4.3 R. Castaing, J.F. Hennequin, L. Henry, G. Slodzian,
The magnetic prism as an optical system.
[2]. R. B. Marinenko, J.J. McGee, 1999 Topical Symposium of the Microbeam Analysis Society,
Fifty Years of Electron Probe Microanalysis: A Celebration Honoring
Raimond Castaing - Introduction, Microsc. Microanal. 7, 93 (2001) 3-219.
[3]. X. G. Jiang, F. P. Ottensmeyer, Optimization of a prism-mirror-prism imaging
energy filter for high resolution electron microanalysis, Optik 94 (1993) 83-95.
M. Barfels, Chromophore Imaging with an Optimized Prism-Mirror-Prism
Energy Filter Designed for an Electroon Microscope, Master Thesis (1997)
University of Toronto.
[4]. L. Henry, Filtrage Magnetique des Vitesses en Microscopie Electronique,
Theses, L'UNIVERSITE DE PARIS 1964.
[5]. S. Senoussi, Etude d'un dispositif de filtrage des vitesses purement
megnetique adaptable e un microscope electronique a tres haute tension,
These, le 3e Cycle, Univ. Paris-Orsay (1971).
[6]. G. Zanchi, J. Ph. Perez, J. Severy, Adaptation of a Magnetic Filtering Device on a One Megavolt
Electron Microscope, Optik 43 (1975) 495-501.
[7]. H. Rose, E. Plies, Entwurf eines fehlerarmen magnetischen Energie-Analysators,
Optik 40 (1974) 336-341.
[8]. H. Wollnik, T. Matsuo, E. Kasseckert, Ein in zweiter Naherung Bildfehlerfreies
Energiefilter fur Elektronenmikroskope, Optik 46 (1976) 255-270.
[9]. S. Lanio, High-Resolution imaging magnetic energu filters with simple
structure, Optik 78 (1986) 99-107.
[10]. J. Bihr, G. Benner, D. Krahl, A. Rilk, R. Weiner, Design of an analytical TEM with integrated imaging
Ω-spectrometer, G. W. Bailey, Ed. Proc. 49th Anual EMSA (1991) San Francisco Press. Inc.
354-355.
[11]. K. Tsuno, T. Kaneyama, T. Honda, K. Tsuuda, M. Terauchi, M. Tanaka, Design and testing of Omega mode imaging
energy filters at 200kV, J. Electron Microscopy 46 (1997) 357-368.
[12]. J. Ph. Perez, J. Sirven, A. Seguela et J.C. Lacaze, Etude, au premier ordre d'un
systeme dispersif magnetique, symetrque, de type alpha, J. de Physique,
Colloque C2, supplement au n°2, Tome 45, fevrier (1984) page C2-171.
[13]. S. Taya, Y. Taniguchi, E. Nakazawa, γ-Type Energy-Filtering Transmission Electron
Microscope, Hitachi Review 45 (1996) 35-40.
[14]. O. Krivanek, C. Ahn, Energy-Filtered Imaging with Quadrupole Lenses,
Proc. XIth Cong. on Electron Microscopy, Kyoto (1986) 519-520.
[15]. O. Krivanek, A. J. Gubbens, N. Dellby, C.E. Meyer, Design and first applications
of a post-column imaging filter, Microsc. Microanal. Microstruct. 3 (1992) 187-199.
|
|