EOS津野の電子光学講座 コンタクト eostsuno@yahoo.co.jp |
|
一方向収束静電プリズム・CDA127CDA127の立体構造。FEMシミュレーション用メッシュCDA127と言うのは静電プリズムに属するエネルギーアナライザで、電子のエネルギーによって 回転運動の半径が異なることを利用して分散を作らせ、検出器の位置に電子をフォーカスさせます。 一様磁場の中で電子は回転運動をしますが、一様電場の中では電子は放物線(Parabolic)運動を します。回転運動をさせるには、同心円内に一様な電場を作ります。内側にプラス、外側に マイナスの電圧をかけます。なぜなら、電子はマイナスのチャージを持っていますからプラス の電極のある方向に引き寄せられるからです。ここでは、具体的な設計に必要な式だけを紹介して、シミュレーションに必要となる数値を 求めてしまいます。 電場の見積もり Uo=5000 V (加速電圧5kV) R=0.045m, Se(電極間距離)=0.012m E1 = 2Uo / Re =2*5000/0.045 = 222222.2 V1=E1*S = 222222.2*0.012 =2666.7V。 左右の電極に、+1333.3Vと-1333.3Vを印加すればよいことがわかります。 ここで大切だと考えられてきたことが、これらの円筒の入り口と出口のところの処理です。 何もしないで電場の計算をして見ますと、図1左のようなポテンシャル分布となります。電場が 外に大きく漏れ出しています。これはあまり良くなさそうに見えます。実際、この種の エネルギーアナライザの設計と言うのは、この入り口と出口、これをまとめてフリンジと 呼んでいます、フリンジ場の処理をどうするかと言うことが、エネルギーアナライザ設計の 鍵を握る事項と考えられてきました。 上に紹介した大島論文にも書いてありますが、このフリンジを詳しく研究したのはドイツの Herzogと言う人で、Herzogのモデルを知っているかどうかが問われたわけです。しかし、これは 数値シミュレーションができなかった時代の話しです。いま、われわれはHerzogさんの世話に ならなくてもエネルギーアナライザの設計をすることが出来ます。 図2は、円筒電極の両側に5°分だけ空間を伸ばし、その前と後に同じ円筒電極を20度分だけ 追加して、但し電圧はかけないでアース電位に置いた場合のポテンシャルを示しています。 このような電極の前後にアース電位の金属を置いて、フリンジ場の調整を行うものを シャントとか、ミラープレート、あるいはシールドプレートなどとさまざまな呼び方が なされていますが、これによって、電場が空間に広く分布してしまうのを防ぐことが 出来ます。 ここでは、円筒をそのまま繋げたのですが、実際に作るときには極率を付けずにまっすぐな ものをつけます。というのも、電極の外では電子は直進運動をしますから回転電極を延ばす ことに意味はありません。ここでは、電場計算のためのFEMメッシュの製作が容易なために、 そのまま円筒を伸ばして計算したのです。 電子軌道の計算は、上で求めた1333Vの付近でいくつかの値で行ってみました。より強い電圧、 1400V, 1350Vでは電子軌道が内側の電極に近づきすぎていることがわかります。弱い電圧1300V の場合は逆に外側の電極の方によっているように見えます。図3が丁度の電圧1333Vを加えた 場合で、このとき初めて両電極の中央すなわち回転半径R=45mmとなっているのがわかります。 計算どおりの値でシミュレーションが進んだと言うことは当たり前のことですが、たいていは 解析的に求めた値と、シミュレーションの値はずれるものだと言う思い込みがありましたので、 今回のこの一致はちょっと意外でもありました。CDA127と言うエネルギーフィルタは、 フィルタ形状としても単純なので、解析解とよく一致するのかもしれません。 ただ、フィルタを出てからビームが水平に進んでいるかどうかについては、水平の場合は ない様にも思えます。これは、シャントの形にも大きく依存すると思われますので、 シャントをきちんと設計して挿入する必要がありそうです。127°と言うフォーカスの角度も シミュレーションでも確かに127°の位置でフォーカスしているように見えます。しかし、 127°と言うのはシミュレーションをやりにくい角度です。と言うのは、入射ビームは水平に 入れてやりますが、出てくるビームは傾いていますから、図では、出てくるビームを水平に するために軌道の図を描いてから図形的に回転して出てくるビームが水平かどうか見やすい ように並べています。ビームは右下から上って行って、水平に出ています。 シミュレーションDisp=12μm / Cos(37°) = 15.68μmここでCos(37°)で割っているのは127°の方向でビームが出ているので、これと垂直な面内で、 分散が起こっていると考えられるからです。見積もった値と比較してみると、37°の補正を 行わなかった値が計算値とよく合っています。ですから、シミュレーションで補正した値は、 計算値より大きな分散を与えています。 エネルギー分解能を求めるには、ビームの入射条件を決めなければいけませんので、前段の レンズの条件などの入力が必要になりますので、ここでは扱えません。その問題はまた別の ところで論ずることにしましょう。 ここで分散を見積もってみましょう。 分散 D = (√2)(2φ2R / π2)δ = 23/2x1272x45 / 1802 x5000 = 12.67 μm と成ります。シミュレーションでは左の図に示したように、ZY面と言うのは、今までの図で縦方向と、 紙面に垂直な方向ですが、この面でのビームの形をプロットしています。電子ビームは、5kVの電圧に対して、 1eVずつ5eVまで減らした場合を計算しています。 作成日 2012/09/25 修正 2014/09/14, 2018/03/14, 2018/12/30 . |
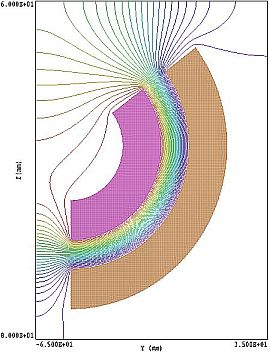 図1.シャントのない場合の電場ポテンシャル。 |
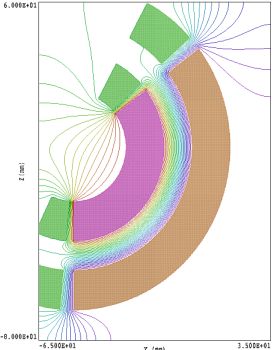 図2.シャントをつけた後の電場ポテンシャル。 |
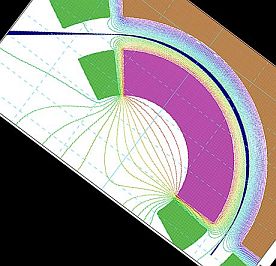 図3.計算どおりの電圧1330Vを加えた場合 |
 図4. エネルギーを1eVずつ変えた5本のビーム |
文献1.目次(エネルギーアナライザ) .アナライザの分類 .飛行時間TOF法 半透明ミラー .CDA127 .SDA180(HDA) .半球アナライザ .TOFと磁気ボトルを使った光電子分光 . 目次(全体)1.最初のページ2.レンズ設計 3.偏向と非点補正 4.光電子顕微鏡PEEM 5.エネルギー・アナライザ 6.Wien Filter 7.収差補正 8. スピン回転器 9.著者のページ |