|
EOS津野の 電子光学講座 Contact: eostsuno@yahoo.co.jp |
ウィーンフィルタは、19世紀の終わりころに発明された荷電粒子の分析装置で、ビームが 直進することから便利な装置としていろいろな分野に応用が試みられましたが、実際 には、ビームがなかなか出てこず、うまく使えない装置として長い時間を空費してきました。 3Dの荷電粒子シミュレーションが容易に出来る最近になってようやくその全貌が明らかに なりましたが、それまでの120年余りの苦闘の歴史を以下にご紹介します。問題は、ビーム 直進の条件であるウィーン条件E1=vB1(E1:一様電場 B1:一様磁場 v:荷電粒子の速度)を フィルターの入り口と出口であるフリンジ場領域において成立させることの困難さと、 荷電粒子(以下、電子と書きますが、イオンについても成立します)が直進せず、それを 探すために多大の時間を対やしなければならなかったことによります。しかし、ここに 問題点であったことが認識されず、3Dの軌道シミュレーションが手軽にできる最近まで、 その原因がフリンジ場に置いてウィーン条件が成立しないことにあることがわからなかった ことによるものでした。私は、1990年ころから当時東北大学教授であった田中通義先生が 獲得した予算の実行のための高エネルギー分解能電子顕微鏡の設計、製作のためにウィーン フィルタを手掛け、その時の設計は失敗であったのですが、田中先生のドクターコースの 学生であった寺内先生(現在東北大学教授)の忍耐強い努力によって、高分解能エネルギー アナライザとしては一応の成功を収めたため、それ以降もウィーンフィルタを使った装置 の設計・製作を続けることが出来、今日まで多数のフィルタの製作にかかわることが出来た ばかりでなく、ツールーズのDr. Hawkesが編集するAcademic Press社のシリーズにThe Wien Filterという表題の本をルーマニアのDr. Ioanoviciuと共著で書く機会も与えられ、数十年 に渡って、Wien Filterについて、設計、製作、解析を行う機会に恵まれました。このため、 今日、Wien Filterのウィーン条件をフリンジ領域においても満たす条件を見出すことに 成功しました。この条件は、一部、Dr.Hawkes編集の本の表紙に記してあります(図1参照) が、其れより良い条件については、最近気が付いたので、ここに記すのが最初です。 この本に記してある条件では、鉄のヨークとコイルによる磁場と同じ鉄による電極で構成 されますが、熱処理の不具合などによるヨーク材質の不均一などによる欠点を排除する ため、空芯コイルを用いたより優れたフィルタの設計をここに紹介します。空芯コイル を使ったウィーンフィルタはこれまでもいくつか提案されてきましたので、新規のフィルタ はそれらの中の一つの型と同じものと考えることもできますが、違った要素も含まれている とも考えることもできるので、新しさと言う観点では微妙なため、特許の申請はしていま せん。ただ、私より前にその形を考案した人の論文では、そのフィルタがそれほど優秀な 性質を持っているものだというところまで解析していなかったことは事実です。現在、この フィルタは北大の触媒研究所の朝倉研究室で稼働中です。そのフィルタを磁場はコイルに よって作るようにと言うことは、そこの朝倉先生によって指示されたもので、磁場をコイル のみでて作ることが最高のウィーンフィルタを作らせるものであることがおかげで証明 されました。 |
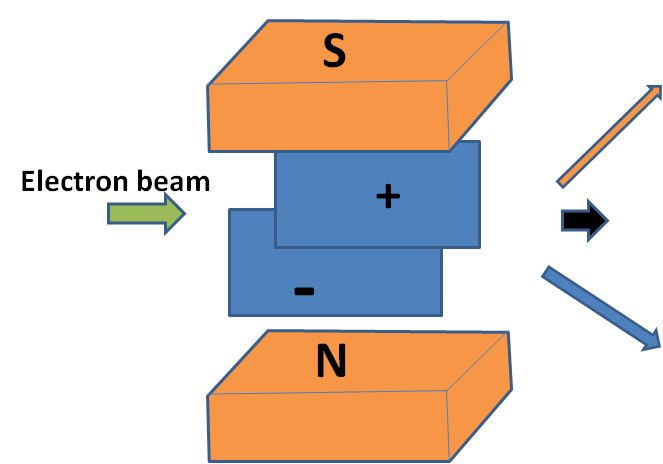
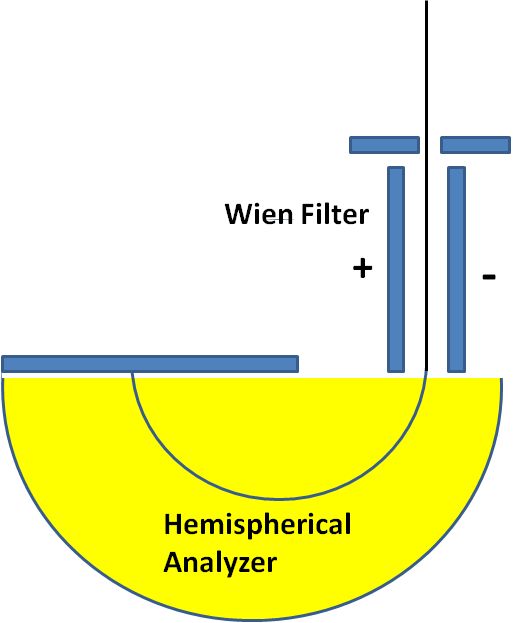
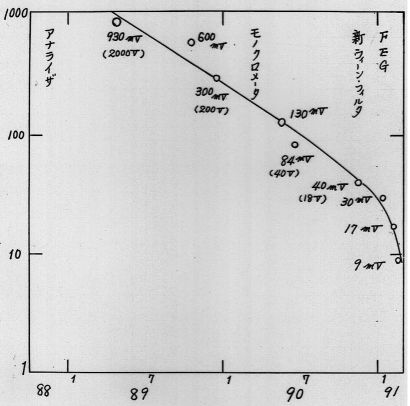
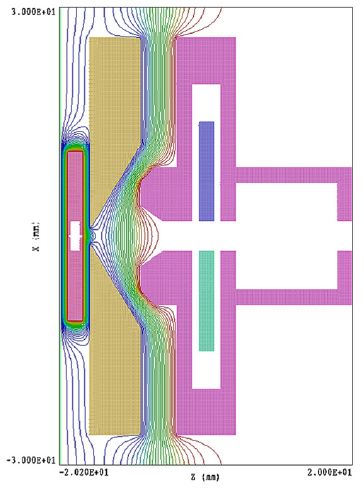
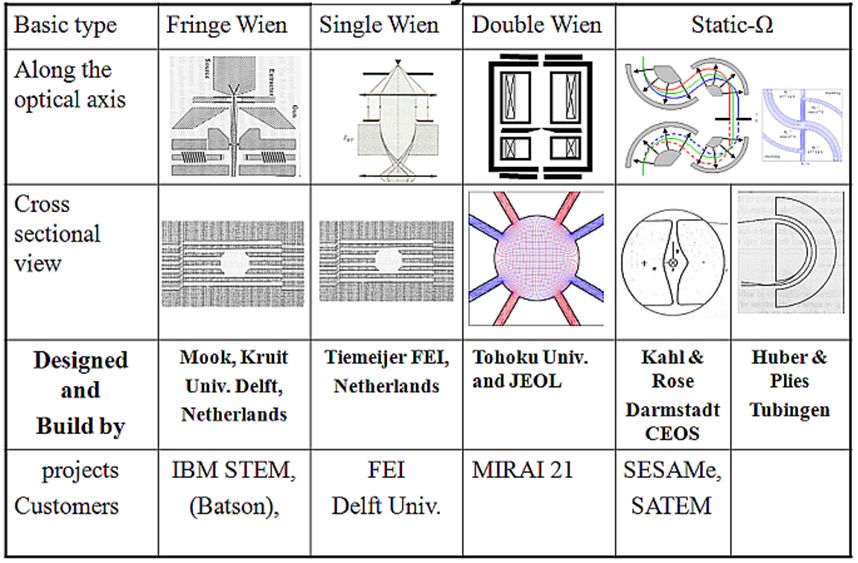
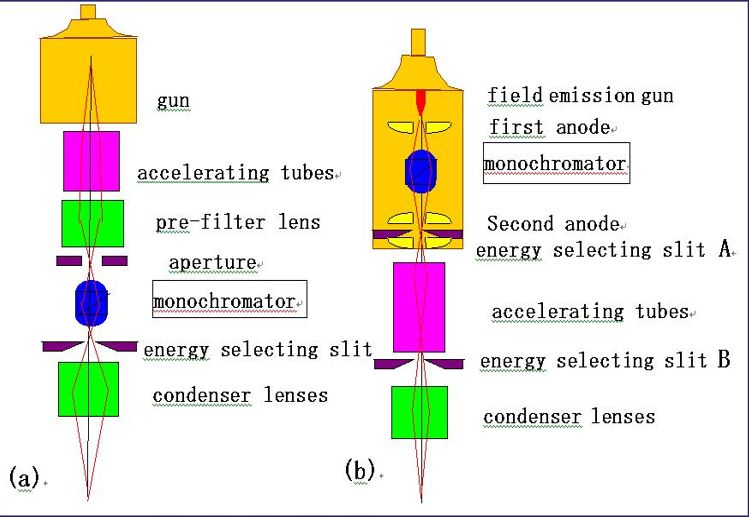
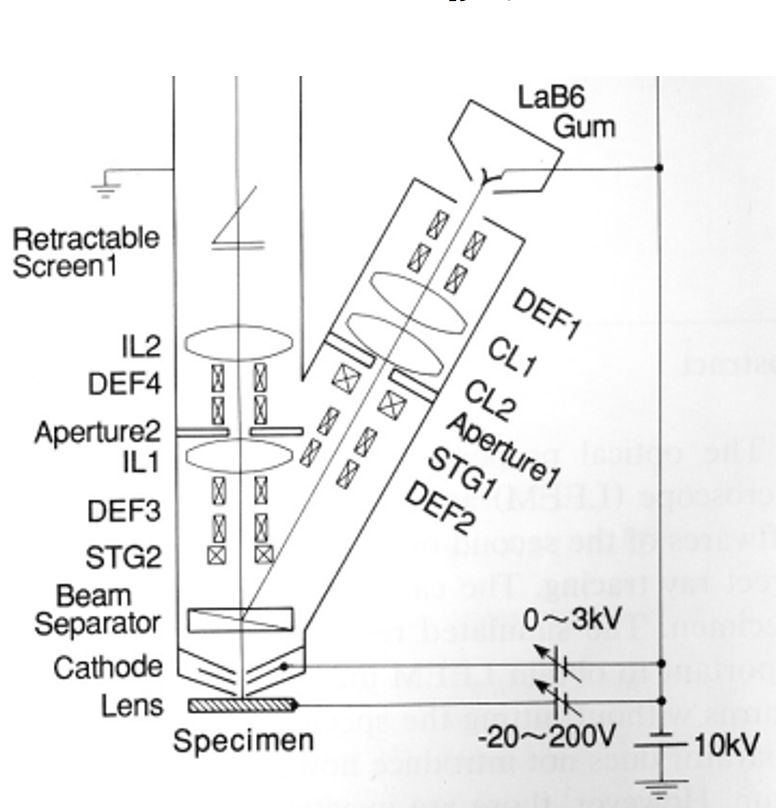
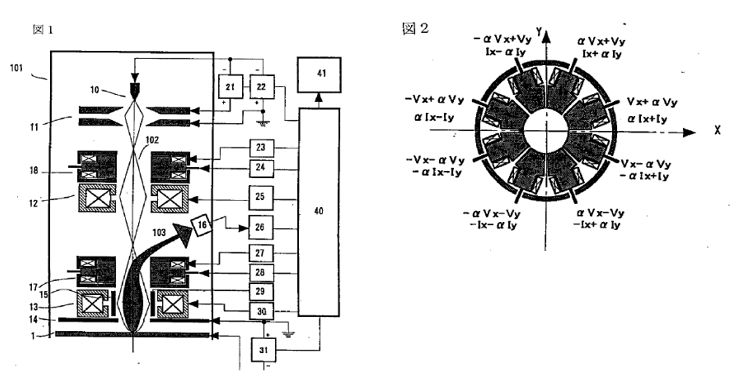
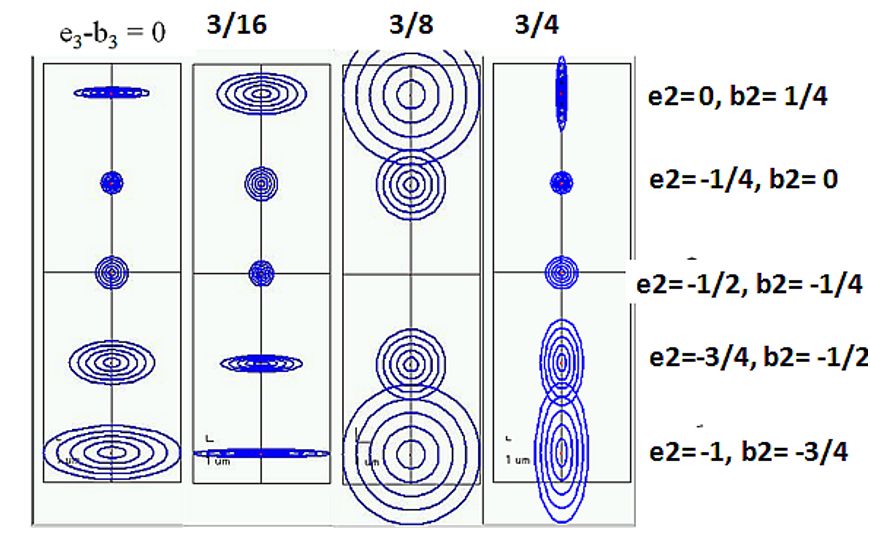
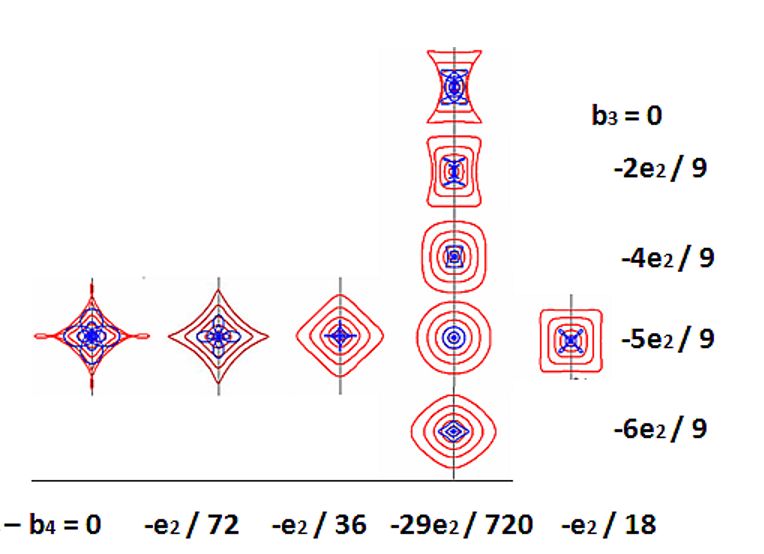
ウィーンフィルタ開発初期の歴史と応用ウィーンフィルタについては、2013年にThe Wien filterと言うタイトルで、Academic PressからフランスはツールーズのDr. Peter Hawkesの編集するImaging and Electron Physicsシリーズの一冊として、出版されました(図0)。共著者は、私のほか、Dr. ウィーンフィルタは、電子発見(1897年)の翌年に発明されています。素早い対応 Damaschin Ioanoviciu先生でルーマニアの研究所の先生です。この本を書くためののように思うかもしれませんが、電子発見の意味するものが何かということや、 準備としてウィーンフィルタ開発の歴史を調べましたので、その結果をここでご紹介このフィルタのその後たどった道を考えると、必ずしも順調な発展ではありません します。ウィーンフィルタは電子やイオンのエネルギーや質量を分析できるフィルタでした。およそ110年からもう少し前の時代、電子線はカソードレイと言う名前で ですが、それらの荷電粒子に加える磁場Bと電場Eの間にその速度をvとしたとき、E=vB知られていました。この頃、真空はガラス管の中の空気をポンプで引いて作られ と言う関係が成り立つとき、それらの荷電粒子は直進するという関係があり、そのていました。初期の頃は、管の中に鳥などを入れておくとすぐに死んでしまうこと 関係はこれを発見したWienの名前を冠してウィーンフィルタと呼ばれています。も知られていました。ガラス管はその後真空装置、電子線装置の真空容器として40 しかし、この関係をフィルタの入り口から出口に至るまで満たすことは大変むつか年位前まで盛んに使われており、大学や会社の研究所では専任のガラス職人を抱えて しく、このフィルタは長い間使われることがありませんでした。荷電粒子のいたものでした。この真空にしたガラス管の中に電極を二本入れ、その電極の間に シミュレーションができるようになってようやく使われるようになったウィーン高い電圧をかけると電極間に雷のようなものが走って輝くことが知られていました。 フィルタの苦難の歴史をお話しします。これが100年前にカソードレイと呼ばれていた電子線です。カソードレイはやがて 電子線と呼ばれるようになります。イオンの場合はカナルレイと呼ばれていました。 以下でお話しするウィーンフィルタの歴史の中で、Boersheらの高エネルギーカソードレイは、負の電荷を帯び、カナルレイは正の電荷を帯びていたと言うわけ 分解能装置に至るまでの長い空白期間に行われた研究についてのお話は、それらにです。 関する文献の探索に、一橋大学イノベーション研究所のスタッフの方のお世話にイギリスのケンブリッジ大学にキャベンディシュ研究所と言う物理学の研究所が なりました。一時期、私はこの研究所の中馬先生のお仕事のお手伝いをしておりあり、ここにJ.J.トムソンがいました。J.J.トムソンが1897年に電子を発見した ました関係で、この研究所のスタッフの方に文献調査のお手伝いをしていただくことで知られており、1997年には電子発見100年のお祝いがキャベンディッシュ ことが出来ました。理科系の大学に機械工作室などがあり、そこの方々が、機械研究所近くのカレッジで開催されました(Kirkland & Brown 1997)。電子の流れで 工作やガラス細工などをやってくださっているのと同じように、文科系の大学であるカソードレイはこの年より前から知られていたにも拘らず、なぜトムソンが ある一橋大学の研究所には、文献調査専門のスタッフがおられました。そこの方電子の発見者として考えられているかという理由は、トムソンはカソードレイの にお願いして、ウィーンフィルタの空白期間とも言える二十世紀初頭から、1980年進行方向に垂直に電場をかけ、電子の進行方向を曲げ、次に磁場をかけてまた 代までに一体どんな研究がなされてきたのかを知る文献を集めることが出来ましたビームを曲げ、両者の比較から電子の電荷eと、質量mの比率e/mの測定に初めて 。Wien Filterはビームが直進する装置のはずでありながら、実験してみると、成功しました。これによって電子には電荷ばかりでなく質量もあることが分かった さっぱりビームが出てこない装置でした。コンピューターシミュレーションにわけです。カソードレイが粒子の集まりであり、光とは違うと言うことが明らかと よってはじめて、この原因が明らかになったわけですが、3次元の計算が自由になったわけです。電子が波でもあることの証明はまだまだ何十年も後のことでした 出来るようになるまで、それがフリンジ場のせいであることはわかりませんで。ただ、エレクトロン(電子)と言う名前は、トムソンの命名ではなく、トムソンは した。従って、1980年代まで、ビームが直進するはずのフィルタでありながら、別の名前を付けたのですが、それは一般には広まらず、別の人の付けたエレクトロン さっぱりビームの出てこないおかしなフィルタである理由がつかめず、厄介な装置と言う名前が広まったのです。 でした。そして、偽科学と結びついたりして、本当の意味で役立つ装置にはなれな かったのです。1980年代までのいわば空白期間ともいえる時代に一体どんな研究が電子の発見は、1897年でしたが、それに先立つ二年前、1895年にレントゲンが なされてきたのかを知る文献を集めることが出来たのは、一橋大学の文献調査X線の発見をしています。こちらは名実ともに発見であり、X線は発見されるや スタッフのおかげです。 多くの人が注目し、色々な応用が試みられました。私がこれから紹介する ウィリイ・ウィーンも自分の物理学の研究者としてのスタートとして、X線の研究 を選び、X-線を発生させるための道具としてのカソードレイ発生装置を作ったの でした。X線は、物質に電子線をあてることによって作られるからです。これは 今でも変わりません。ウィリイ・ウィーンは発生させたカソードレイに電場と磁場 を直角方向から当てる装置を1897年に作り (図2参照)、1898年にトムソンと同じ 、e/mの比を測定した論文を発表しています[Wien 1898]。トムソンに遅れること 一年であったため、ウィーンは、電子の発見者としての栄誉を逃したわけです。 ウィーンは電子の進行方向(これをZ方向とする)に直交して電場(この方向をXと する)と磁場(この方向をYとする)をそれぞれ加えました。ウィーンの方法が トムソンの測定に比べてエレガントで、電場と磁場を同時に直交してかけ、電子が 真っ直ぐに進むように値を調節したからでした。トムソンがそれぞれの場を別々 に加えて、どれだけ曲がったかを測定したのに比べて、ずっと精度の高い測定の 出来る方法でした。電子の発見者としての栄誉と、ノーベル物理学賞はトムソン の物になったわけですが、ウィーンは別の研究で1911年にノーベル賞を受賞して います。物質が熱せられる時に発生する光の色、波長の研究に関してです。鉄が 熱せられると赤から黄色、ついには白く色が変わっていくそのスペクトルの変化 に対するものでした。トムソンがイギリスの物理学研究のトップを極めたのに 対して、ウィーンがドイツの物理学の頂点を極めた人であるという点は変わら ないわけです。ただ、トムソンが電子の人でウィーンはイオンの人という分類 も当たりません。トムソンは、イオンの質量を測定する質量分析装置でもそれを 初めて使った人として考えられる場合もあるからです。 このe/mの測定にウィリイ・ウィーンが使った装置がやがてウィーンフィルタと言う 名前で呼ばれるようになる装置であり、ウィリイ・ウィーンが電場と磁場を調節 してカソードレイを直進させた条件がウィーン条件と呼ばれています。しかし、 ウィリイ・ウィーン自身は、その後の物理学研究の生涯の中で二度とウィーン フィルタを使うことはありませんでした。ウィリイ・ウィーンの研究が、イオン から離れたわけではありません。彼の研究の中心はあくまでもイオンにありました。 ウィリイ・ウィーンの生涯と彼のイオンビーム研究の軌跡についてはその後1998年 のウィーンフィルタ発明100年の記念の年にブラジルの電子顕微鏡学会で行われた 記念行事に彼の一族の人が講演した記録が残されており、その時の論文は インターネット上で公開されていますので、ウィリーウィーンの生涯に関心ある 方は参照下さい。[Wien K. 1999]。 2.質量分析の補助装置としての初期のウィーンフィルタウィリー・ウィーンの発明から30年、ウィーンフィルタの利用に関する論文は 見当たりません。最初のウィーンフィルタの実験報告は、アメリカのフランクリン 研究所のBainbridgeから1932年に出ています。この論文は実験結果の報告で、装置 の詳しい説明はその翌年、1933年にJournal of the Franklin Instituteに述べ られています(図3参照) [Bainbridge 1932, 1933]。この装置は質量分析装置 (Mass)として使われました。質量分析装置は1910年代に発明されましたが、1930 年代に盛んに使われるようになった背景として、アイソトープの発見があります。化学的方法では分離できない物質でありながら、質量と言う物理的性質の異なる ものがあると言うことは1906年に見つかったのですが、周期律表の同じ場所を 占めるこのような元素をアイソトープと呼ぶようになったのは1913年のことでした。 アイソトープは最初ラジオアクティブと言われる放射性元素で見出され、放射性 同位元素と呼ばれました。Astonと言う、質量分析装置の元祖のように考えられて いる人がアイソトープは、放射性元素に限らず、たいていの元素にあると言うこと を示しました。このように元素の質量を測定することが、アイソトープの発見に 不可欠であったわけです。1930年代は、まさに色々な物質に対してのアイソトープ 研究の時代であり、丁度このころ発展しつつあった質量分析装置の質量分解能 がアイソトープを分離することが出来るレベルにあったわけです。 質量の色々混じった物質から特定の質量の元素を分解して測定するための質量 分析装置としては、イオンを一様磁場の中で180°回転させる電磁石が使われて いました。正確な測定には、測定器に試料が入る前に測定されるイオンの速度を 一定にしておかなければなりません。 そこで、この電磁石の前にイオンの速度を一定範囲に制限するための速度分離 装置が付けられました。Astonの装置では、これは電場偏向器でしたが、 Bainbridgeは、この速度分離器としてWien フィルタを使った のです(図3参照)。 ところが、Bainbridgeの論文には、Wien フィルタと言う言葉も、Wienの論文の 引用もなく、その後のアメリカの他の人たちの論文でもそれらの引用がありません。 恐らく、Bainbridgeは、Wienとは独立にWienフィルタの発明をしたのではないかと 思われます。ただ、Bainbridgeが速度フィルタとして使ったExBフィルタが ウィーンフィルタであると言うことは、論文内の記述から明らかで、ビームの直進 条件(ウィーン条件)も示されています。 所が、事情はそれほど単純ではありませんでした。質量分析装置に使用する電場 磁場重畳場には別の流れがありました。127°偏向型の静電フィルタに垂直に静磁場 を印加すると、イオンビームのフォーカスがシャープになると言うことで、直交 電場と磁場(ExB)をイオン分析装置に使う論文が同じ1930年代に多く見受けられる ようになったのです。このExB型フィルタは、電子ビームを直進させるわけではなく、 従って直進条件であるウィーン条件も出てこないので、ウィーンフィルタではあり ません。最初の論文は、1929年のPhysical Review誌に出た論文で、Path of charged particles in electric and magnetic fieldと言うタイトルでした [BartkyとDempster 1929]。オーストリーのBondy and Popper[1933], 同じく Shaw(シカゴ)[ 1933年、1938]、Bleakney and Hipple Jr. (プリンストン)[ 1938] などの論文があります。しかし、この方式はやがて質量分析装置としては消えて しまうので、電場偏向型の質量分析装置に磁場を重畳するとフォーカス性能が向上 すると言う説は正しかったのかどうか怪しいものです。科学の世界にはこうした 偽科学とでもいうようなものがしばらくは続くことがあります。そして、それらが 本物と区別なくしばらくの間、引用されていくのです。ウィーンフィルタの引用 文献にもこれらのいくつかが引用されています。ただ、90°偏向電磁石に90°偏向 円筒電極を重畳する装置は、スピン回転器として現在利用されています[Nagai et. al. 2011]。あとで示しますように、スピン偏向器は、本当のウィーンフィルタの 応用としても使われていますが、ビームを90°曲げた方が便利な場合もあり、その 時電場と磁場を重畳した90°偏向器が使われているのです。どちらが沢山使われて いるかと言うと、半々くらいだと思われます。従って、電場と磁場を重畳すると、 質量分析装置の分解能が上がると言う話はウソであったにしても、そこで使われた 装置と同じものは現在別の目的でよみがえっているわけです。 一方で、Bainbridgeに始まるウィーンフィルタは例えばJordan(イリノイ)[1940, 1941]の論文The mass differences of the fundamental doublets used in the determination of the isotopic weights C12 and N14、 など数は少ないものの アイソトープと関連した測定に用いられていきました。 アメリカとは異なり、ドイツでは1934年に二つの論文が出ています。一つは HennebergのAnnalen der Physikの論文[1934]で、「速度と質量分析のための 重畳場」と言ったタイトルで、場の重ね合わせを行った装置についての速度 フィルタ、質量フィルタの理論で、最後にWienの方法という言葉が出ています。 もう一つはHerzog[1934]の「円筒レンズとプリズムについてのイオンと電子光学 」と言うタイトルのこれも理論ですが、電場や磁場の色々の場合の質量や速度 フィルタのことが述べられています。その中で一章を割いて、特別の場合として Wiensche Geschwindigkeitsfilter ウィーンの速度フィルタ、括弧して補正光学 系と題されています。この論文の中で、先ほど紹介したBainbridgeの論文が引用 されています。しかし、Willy Wien の論文の引用はありません。つまり、1930年 代において、ドイツでは電場と磁場を重畳した速度フィルタがウィーンフィルタと 呼ばれていたわけですが、ウィーン自身の論文は引用されていないこと、アメリカ で使われていた速度フィルターは逆にウィーンフィルタの分類の中でドイツでは 引用されています。しかし、ドイツでは、ウィーンフィルタが実験に使われる ことはなかったようです。電場・磁場フィルタの解析があって、その続きとして 両方を重ね合わせたり、つなぎ合わせたりした場合も理論的な解析の対象となり、 重ね合わせて、さらに電場と磁場によるビームの偏向をキャンセルした特別の場合 がウィーンフィルタと呼ばれていたということになります。1940年代50年代は、 重畳場を用いると質量分析のビームのフォーカス特性が良くなるという論文は アメリカで出続けますが、逆にウィーンフィルタを使った装置の論文は見当たり ません。 3.Boerschらのウィーンフィルタの電子への応用とその電子顕微鏡への接続ウィーンフィルタがその威力を発揮する使い方をされるのは1960年代に入ってからで、 Boersch, Gaiger[1962, 64, 66]らによって、電子による高分解能エネルギー アナライザとして登場します。このベルシェらの装置こそがウィーンフィルタの 最初の利用と言っても良いほどのもので、この装置なくしてウィーンフィルタの その後はなかったと言ってもよさそうです。 今、ウィーンフィルタ発明から120年近くの歳月が流れていますが、その半分の 歳月をいわばウィーンフィルタは空費したと言っても過言ではありません。この 時までの60年間の使い道は、質量分析装置の前段階に速度フィルタとして取り付け られるといった程度の利用が高々数件と他の場合も入れた理論が数件作られていた だけと言った状況でした。その発明から60年を経てようやく同じドイツの著名な 電子線の物理学者であるベルシェによって花開いたのです。しかも、その時実現 したエネルギー分解能は、その数十キロボルトという高い加速電圧に対しては 今日まで破られることのない最も高い値を突然実現したことになります。 Boerschらの装置が発表になると、1960年代、70年代を通じて、沢山のウィーン フィルタ関連の実験・理論[Ioanoviciu 1973]の論文が出るようになりました。 これ以降、Wien filterを使った装置はWien filterと呼ばれ、Wienの論文も引用 されることが多くなったわけです。 ところで、装置としてのウィーンフィルタは、電場と磁場を重畳して加える必要 から、電極の形状に制約が生じ、一様電場が作り難い欠点がありました。電極の 自由な形状を妨げない磁場装置の開発が一つの課題でありました。さらには、この フィルタにはレンズ作用を伴いますが、一様磁場と一様電場のレンズ作用は、電場 方向(X方向)のみで、このようなレンズのことを円筒レンズと言います。初期の Boerschらの装置は、フィルタの前または後ろにY方向にレンズ作用をする円筒 レンズを置いてフィルタのX方向への円筒レンズ作用と組み合わせて、非点なし 結像をさせる装置でありました。やがて、ウィーンフィルタに4極子場を組み合わ せることによって非点なし結像をさせることが出来ることが明らかとなり、一様 電場磁場に電場または磁場の4極子場を加えた装置が使われるようになりました [Andersen 1967, Legler 1963]。 レンズの収束作用が向きによって異なる場合を非点と言います。人の目の場合も 同じ現象があり、乱視と呼ばれています。非点なし結像と言うのは、このような 非点がなく、あらゆる方向に同じ強さの収束をすることを意味します。ただこれは、 焦点があった場所でだけ実現すれば良く、途中では方向によって違うレンズ作用で あってもかまいません。常に方向に寄らず同じレンズ作用をする場合をラウンド レンズと言います。この場合は、物面(観察している対象のことを言う)から像面 (フォーカスした面)までのレンズ作用が方向に寄らず一定になります。 ウィーンフィルタでは、一様場の生成と非点なしフォーカスのための4極場の生成が まず関心事項であり、続いて、二回フォーカスをさせることによって、収差と分散 をキャンセルさせることが分かってからは、二回フォーカスの実現法などが問題に なりました[Andersen & Le Poole 1970]。また、エネルギー分解能を大きくする ために、フィルタ内でだけ電子の速度を落とす、リターディングのテクニックが 使用されていきました。Boerschらの装置では、このリターディング法によって高い エネルギー分解能が実現しています。最後に、ウィーンフィルタのウィーンフィルタ であるゆえんである、ビームの直進条件がフィルタの入口と出口(これをフリンジと 呼んでいます)で、満たされなくなることに対する対応策が重要な問題点として認識 されたのは最近のことです。 ウィーンフィルタが長い間うまく使えなかった原因は、この問題点、フリンジ場で のウィーン条件維持が技術的に難しかったにもかかわらず、これが問題であると いう認識が長い間なかったことが上げられます。最も高度な光学機器として使われ ても良かったウィーンフィルタが長い間簡単な光学機器としての利用しかされて こなかった原因がここにありました。つまり、ウィーンフィルタはビームが直進 すると言う便利な光学機器のはずでありながら、実際に作って実験すると、ビーム がなかなか出て来ない奇妙な光学機器であり、その原因がなかなかつかめない ものでした。そして、理論は理論でウィーン条件が全体で満足されていると言う 前提で作られているにも拘らず、実際の装置では、例えビームが最終的に出てきて いたとしても、ウィーン条件が狂っているものを補正してビームを出している ので、実験では理論が予想するような結果にはるかに及ばず、理論が全く役に 立たない状態にあったことも、ウィーンフィルタの発展を阻害してきた大きな 原因と今では考えることが出来ます。 以下では、ウィーンフィルタの色々な応用分野について述べます。ただ、ウィーン フィルタは、電子線のみならず、質量分析装置や核物理装置にも応用されて いますが、著者の専門は電子線であり、これらの二分野には知らないことが 多いので、以下の応用は電子線に限ることにします。 4.ウィーンフィルタを搭載したTEMの東北大・田中研への納入私が、ウィーンフィルタの開発を命じられたのは、1986年でした。東北大学の 田中通義先生が私の勤め先であった日本電子株式会社との共同研究としてミリ ボルトと言う高エネルギー分解能の局所分析の出来る電子顕微鏡を開発する予算 を獲得したことに始まりました。このウィーンフィルタを使ったミリボルトの エネルギー分析の出来る電子線分析装置は、ドイツのベルシェが1962年に開発し、 1980年代に至るまで色々な工夫を凝らして、改良がくわえられてきた装置です [Essig 1981, 1986]。京都の電子顕微鏡国際会議にやってきたEssigに学会期間中 に詳しく彼らの装置について聞く機会があり、それが結局はBoerschらの装置を 次につなげることになったと今では思っています。Boerschらの作った高エネルギー分解能ウィーンフィルタ装置をまねた装置を電子 顕微鏡上に作り1991年に東北大学に設置しました。装置は、まず図5(a)の電子 顕微鏡にアナライザと呼ばれる試料を通過してきた電子線の試料によるエネルギー ロスを測定する装置を取り付けました。これが(b)です。続いてモノクロメーター を作り、これを電子銃の下に取り付けました(c)。これは、 電子銃から出てくる電子ビームがあらかじめ持っているエネルギーの幅を制限し、 狭いエネルギー幅の電子線のみを試料にあててやるための装置です。これらの エネルギーアナライザとモノクロメーターにはウィーンフィルタを 用いたわけです。(d)は電界放射型(Field Emission)電子銃(gun)と言うエネルギー の広がりの小さい、明るい電子源を搭載した電子銃を用いました。Boerschらの 装置は、電子顕微鏡の機能は持たなかったのですが、我々は電子顕微鏡の機能を 付け加えた装置に発展させたわけです[Terauchi et al 1990]。 このような装置の改造によるエネルギー分解能の向上の様子を図4に示します。 この間、ウィーンフィルタ自身の形状にも工夫が施され、分解能の向上を助け ました。最終的に到達したエネルギー分解能は、12meV(一度だけ試料を入れない 状態で9meVが出ましたが、試料を入れた場合の再現性のある分解能としては12meV となりました)で、これはBoerschらの値には及ばなかったものの、同一水準の 分解能を達成し、その後長い間、透過型の装置で稼働している装置としての世界 最高のエネルギー分解能を保持していました[Terauchi et. Al. 1999]。この 装置は、まだWienフィルタについて十分な理解がなされていない時代に作られた ものであり、特に、フリンジ場でウィーン条件が満たされていないことに対する 理解が十分でなかったため、ビームを系全体に通すことが難しく、忍耐強いビーム 探しが不可欠でしたが、田中先生のドクターコースの学生であった寺内先生(現在 東北大学教授)の忍耐強いビーム探しがダメなWien フィルターを使いながらもそれを 搭載した装置の高分解能エネルギーアナライザとしての開発を成功させてくれた ことが私の日本電子内での他の先生方から発注された、別の目的のWien Filter 搭載機の担当者にさせ、定年後のコンサルタント業においてもいくつかの設計 を手掛けることにつながり、図1の本を書くことにまでつながり、その表紙に 掲げたフィルターの設計に至り、フリンジ領域においてもWien条件を満たす フィルターの設計にまで至ることが出来たものです。 しかしながら、東北大学のこの装置は、あまりにも複雑で、オペレーションの スキルも高度なものを要求され、製作にもリスクが大きかったことから、後に 続く装置がありませんでした。この装置を見た多くの人は、自分たちも同じような 仕事をすることをあきらめるに十分な装置だったとも言えます。このような状況 の中、オランダのデルフト工科大学のKruitは、大学院の学生であったMookをこの 装置が設置してある東北大学にしばらく派遣し、装置を詳細に調べた挙句、新しい 装置のアイデアを発表しました。その意味では、ドイツで初めて作られた装置は、 日本を経てオランダで花咲いたということが出来ます。 Kruitの発表したモノクロメータ[Mook & Kruit 1997]は、電子銃内にそれを設置 するというものでした。Boerschの装置と、東北大の装置では、電子銃で加速 された電子ビームをモノクロメーターに入る直前で減速していました。これが一つ には、装置を大掛かりなものにする原因となっていました。電子銃の中では、電子 ビームは、最初数ボルト以下で物質中から真空中に放出された電子を加速して います。FEGの電子銃では、いったん引き出し電極と呼ばれる電極で5kV程度に加速 してから、陽極との間で所定の加速電圧まで、加速されます。Kruitのモノクロ メーターは、ウィーンフィルタをこの引き出し電極と陽極の間に入れました。 こうすることによって、いったん加速した電子を再び減速して使い、もう一度加速 して試料にあてるという無駄なことをする必要がなくなりました。少なくとも 数十キロボルトあるいは100kVから減速する必要はなく、5kVからでよいので減速 の程度が低くできました。これ以降の全てのモノクロメーターは、この電子銃内 モノクロメータとなりました。この方向性は、装置の小型化という意味では優れた 考えでありましたが、装置オペレーションの困難さを解消するという意味では 誤解に基づくものでありました。この当時、東北大のモノクロメーターの オペレーションが大変であったのはリターディングが大きいせいだと考えられて いたため、それを出来るだけ少なくする工夫として電子銃内モノクロメーターが 考案されたのですが、実際には、オペレーションの大変さは、電極と磁極の形状 の違いによるフリンジでのウィーン条件の不一致にこそその最大の原因があった のでした。 さて、Kruitのモノクロメータをシミュレートするのに使った図は、図6に示しますすが、 このモノクロメーターに対するKruitの考え方は次のようなものでした。まず、分散は ビームサイズより大きければ良いというのが第一点です。FEG(フィールド エミッション)電子銃から出てくるビームのサイズは数十ナノメーターと言われ ています。Kruitの考えからすると、モノクロメーターのエネルギー分散も 収差がなければ、数十ナノメータで良いことになります。ただ、問題はスリット の幅も数十ナノメータにしなければならないことです。分散が数十ナノ メーターで良ければフィルタのレンズ作用はごく小さくて良いので、収差が発生 する以前にとどめることが出来ます。結局、ナノメータースリットさえ作れれば、 このような非常に弱励磁のフィルタはモノクロメータとして魅力的だと言うことに なります。 この装置はデルフト工科大学で完成したものが、IBMのヨークタウンハイツの Batsonの研究所に納入されました。デルフトでこの装置を作って学位を取った MookがしばらくIBMに滞在して納入を行いました。Batsonは、はじめ学会で紹介 していました[Batson 1999]が、そのうちにモノクロメーターは装置から外され ているといううわさが流れました。やがて、何年かして、島津のマンチェスター にある研究所がこのモノクロメーターの権利と一台を買い取り、日本に運んだ と言われています [Cublic et. al. 2004]。テストは東京で行われていたと うわさで聞きましたが、日本に来てからの学会発表はありませんでした。 FEIは、モノクロメーターの商用機を最も早く出したメーカーです。デルフト工科 大でKruitの前任の教授はフィリップスのfan der Mastであったことからもわかる ように、フィリップス、やがてFEIは、デルフト工科大学と強いつながりが あります。ウィーンフィルタを利用したモノクロメーター開発でもKruitの指導が あったと推定されますが、FEIではMookのフリンジフィールドウィーンフィルタは 採用せず、独自のフィルタで商用機を作りました。ウィーンフィルタの断面図は 、FEIから出ている論文には一切掲載されていませんが、学会発表のスライドで 紹介された図面では、Mookのウィーンフィルタと同じ断面形状をしていました。 つまり、FEIは、デルフト工科大学のウィーンフィルタの形は採用しましたが、 Kruitの考えは退け、普通の一回フォーカスウィーンフィルタを商用機として 採用したものと思われます。これは、賢明なことでした。ナノメーターの隙間 しかないスリットを使った場合、コンタミがスリットの隙間についた場合などを 想像すると、安定な装置として商品にはしにくいと考えられるからです。FEIは 単純な一回フォーカスのウィーンフィルタを電子銃内モノクロメーターとして 採用し、スリットはアース電位上に置くことが出来たので、構造も簡単で2000年 代初期にモノクロメーターの商用機開発に成功し、それからしばらく独占的に モノクロメーターの販売を行いました。 日本電子は、これに対し複雑なモノクロメーターを開発していました。モノクロ メーターの第一号機は分析装置用として東北大学から、第二号機は高格子分解能用と してオックスフォード大学から受注していましたが、いずれも自由な設計を 許されず、レベルの高い要求に悩まされました。このため、高度な設計を行わ ざるを得ず、完成まで多くの年月を費やすことになってしまいました。いずれの 場合も収差のキャンセルが出来る二回フォーカス型のフィルタとなりました。 二回フォーカス自体は特に難しくはありませんが、二回フォーカス後には収差の キャンセルの他に分散もキャンセルされるため、エネルギー選択のスリットは 一回フォーカスの位置に入れなければなりません。モノクロメーターは、電子銃の 中に入っていますので、それは200kVの高電圧中にありました。ここに、 機械的な動きの必要なスリットを入れることは大変なことでした。その他、ビーム の調整も何個もの細い穴をすり抜けて通さなければならず、調整に困難を極め ました。(!--図6には、二回フォーカスをさせたときの電子軌道と、東北大用として 開発したウィーンフィルタと類似のフィルタの断面を示してあります--)。この フィルタは私が担当していた時代には、このような困難が続きましたが、 その後、うまく動作できるようになり、何件もの客先で稼働していると聞いています。 一方、Zeissはモノクロメーターとして、Wien フィルタを採用しませんでした。 Zeissは、静電型オメガフィルタと言うこれも複雑なモノクロメーターを開発 しました。このモノクロメーターを開発したダルムスタット工科大学のドクター コースの学生は、なぜ静電型オメガフィルタなどと言う複雑なものを採用したのか と質問したところ、電子銃内は高真空にしなければならないのでコイルを巻くことが 許されないため、静電型にせざるを得なかったと答えてくれました。 FEIも、日本電子もウィーンフィルタを採用し、従って電場だけでなく磁場も 使っていましたので、当然コイルを高真空中に入れていますが、この学生は 教授に強くコイルはダメと言われていたので、静電型にせざるを得なかったのだ と言っていました。ダルムスタット工科大学は、シェルツァーの大学であり、゜ その弟子であったRoseが長く教授を務めていましたが、その間Roseの設計した エネルギーアナライザはZeissで製品化されました。しかし、Roseの主な研 究対象であった収差補正装置は、Roseの在任中は実験的成功をおさめず、Rose の研究室はRoseの定年と共に閉鎖となりました。こうして、ドイツの電子光学 研究の中心は、Roseの最初の弟子であったPliesのチュービンゲン大学(Pliesも 今では定年となったので、ここも今では電子光学の中心ではなくなりました。 かつては、日本の大学で電子回折の研究をした多くの先生方の一番の留学先 であったチュービンゲン大学も電子光学研究の中心地から外れてしまいました) と、これもRoseの弟子であったハイデルベルクにある欧州共同体の分子生物学 研究所を辞めて収差補正装置の会社CEOSを設立したHaiderとZachの所に移ったと 言えるでしょう。ここには、Roseの最後の弟子たちも何人か入社し、ドイツ電子 光学の中心をなしているのではないかと思われます。この点、日本では、日立には 名古屋大学と大阪大学の後ろ盾がありましたが、日本電子には電子光学の指導を 担当した大学は日本国内にはなく、新しい技術の導入に当たっては、オックス フォード大学からの受注に伴う、技術指導、あるいはドイツの大学で書かれた 学位論文の図を見て装置を作らざるを得ませんでした。 5.ウィーンフィルタのビームセパレータへの応用試料に対して垂直にビームを入れ、試料からまた垂直に反射してきたビームの作る 像を見ようとした場合にどのような方法があるでしょうか。ビーム発生源である 電子銃がまず必要で、それを試料にあてるためのレンズ系も必要です。反射ビーム は、何もしないでそのままフィルムに記録すれば良い場合には、方法がありました。 LEEDと呼ばれる装置では、フィルムの真ん中に穴をあけてこの問題を解決しました。 試料に入射するビームは、この穴を通って試料に達します。試料で反射したビーム は、いろいろな角度に広がることと、穴を通り抜けて直進する電子は情報を持た ないので、フィルム上に止まって感光した電子から電子回折の情報が読み取れました。 これがLEED即ち、Low Energy Electron Diffractionと呼ばれる装置です。 LEEDの場合は電子回折図形なので、一定距離だけ離したところに像検出器を 置けばよかったのですが、LEEM即ち、Low Energy Electron Microscopeになると、 反射ビームに対しても像を作るためのレンズ系が必要でした。この場合、入射 ビーム用のレンズ系と、反射ビーム用のレンズ系とが同じ場所に必要になり ますので、両方の軌道を分けてやる必要が出てきます。この目的に使われるのが ビームセパレータで、ウィーンフィルタもこの目的のために使われました。ビーム セパレーターとしては、セクター磁石と呼ばれる電磁石を使うことも出来ます。 ただ、セクター磁石を使う場合は、試料の面に対して入射ビームも反射ビームも 傾斜して置く必要がありますが、ウィーンフィルタを使う場合には、反射ビーム 用のレンズ系は試料に対して垂直に置くことが出来ます。垂直に置ける一番大きな 利点は装置の安定性であり、収差も小さく出来ます。 ビームセパレータは、ウィーンフィルタの原理をそのまま利用したような応用例 で、ウィーン条件と呼ばれるビームの直進条件が、 E1 = vB1 , と書かれます。ここで、E1 は、一様電場、 vは電子の速度、 B1は一様磁場の強さ を表します。電場と磁場の強さが電子の速度で結び付いています。ビームセパレータ はこの式のvの符号を利用したもので、速度には向きがあるため、ビームの向きで ウィーン条件が合う方向と合わない方向が出てきます。図10に示すLEEM装置[Tsuno 1994]で、試料から反射したビームが進む方向をこの式に表わされるvの正の方向 だとしますと、この方向に進む電子はウィーン条件が満たされているので直進 します。ところがLEEMに入射するビームの方はvの方向が逆になってしまいます。 逆向きなのでマイナスvとなって上の式は満足できません。E1は、-vB1とは等しく ないのです。そこで、ビームは曲がってしまいます。この曲がりの角度が図10に 示すLEEM装置の場合には30°になるようにウィーンフィルタの電場と磁場の強さを 調節してあるわけです。反射ビームは直進するので、角度は関係ありません。その後、 いくつかのWienビームセパレーターを使ったLEEM装置が発表されています[Miyoshi et. al. 1999, Shimakura et. al. 2008]。 ウィーンフィルタをビームセパレータに利用した装置がもう一つあります。それは、 イマージョン型と呼ばれる磁場の中に試料が入っている高分解能型のSEM(走査電 子顕微鏡)です。この一例を特許の中の図から拾って図11に示します。原理はLEEM の場合と同じです。ただ、今度は直進する方のビームが一次ビームになります。 電子銃からレンズ系を通ってきたビームがウィーンフィルタを通過するときに ウィーン条件を満たすように電場・磁場が合わせておきます。こうすると、試料 から出た二次電子は速度vの向きが反対になるので、ウィーン条件を満たせず、 電子は検出器の方に曲げられるのです。 この仕組みの中に、他にもいろいろな工夫が込められています。試料から出た 二次電子のエネルギーは入射電子のエネルギー(30kV~1kV)と比べて低い値(1~50V) です。このため、対物レンズの磁場の中で、らせん運動をしながらレンズの上の 方に引っ張り上げられます。らせん状に回りながら上がっていくが、レンズの中に 入って磁場がなくなると、そこで広がってしまいます。広がった二次電子がレンズ の壁にぶつかって消えてしまいます。そこでレンズの穴の内側には電極が入れて あって磁場で吸い上げた電子を今度は電場の力で、対物レンズの上まで持ち上げる 仕組みになっています。これを二次電子のスルーザレンズ方式と呼んでいます。 そこでやっとウィーンフィルタの登場になります。対物レンズの真上に置かれた ウィーンフィルタで曲げられた二次電子は電極の方向に曲がるので、電極に ぶつかってしまいます。そこで、日立のSEMでは、片側の電極を網で作り、二次 電子がこの網をすり抜けて検出器に向かうことが出来るようにしてあります。 この網はもう一つの役割があります。検出器は電子を集めるために8~10kV程度の 電圧をかけて電子を引っ張り込む働きをしていますが、この電場が漏れて 光軸にまで達すると、一次ビームの軌道に影響を及ぼします。網があることで、 この強い電場が光軸の方にまで伸びて来ず、網をすり抜けてきた電子だけを集める ことになるわけです。 おそらく、このビームセパレータとして使われているウィーンフィルタが世界で 使われているウィーンフィルタの90%以上を占めているのではないかと思われます。 ビームセパレータだけが大量生産されている唯一のウィーンフィルタであると言える でしょう。不思議なことにこのビームセパレーターについてはオリジナル論文が ありません。日立の人が書くSEMの一般的な解説記事にはこのウィーンフィルタが 紹介されていることが多いのですが、引用文献がありません。その理由は、この 仕組みをSEM上で実現した人とアイデアを提供した人が異なっていたためであると いうことが中馬先生の取材で明らかとなりました。日立ハイテクでこの装置を実現 した人は自分のアイデアではなかったため、その結果を論文にせず、アイデアを 提供した日立中研の人は単なるアイデアで実験もしていなかったので論文にする ネタもなかったということのようです。さらには、相談に行ったときに教えて もらったそのアイデアをその時は重要なものであることに気づかず、後になって そそれがスルーザレンズデテクタに最適の仕掛けであることに気付いたのだそうです。 図11に示してあるビームセパレーターは、実はさらに次の段階のものを示しています。 それは、低加速電圧SEMの普及によって始まりました。低加速電圧SEMは、絶縁体や 半導体の試料でもチャージアップが起こらないと言うことで急速に普及してきた SEMです。その理由は、加速電圧が1~2kVの間くらいで、入射する電子ビームの量に 対して、反射ビームや二次電子などを合計の出ていく電子の量が丁度つりあうと 言うことが分かったからです。入ってくる電子と出ていく電子が同じ数であれば、 入ってきた電子を導電性の物質を通して外に逃がしてやる必要がありません。半導体 や絶縁体のように電流が流れない物質に電子ビームを当てても、入射した電子が 試料中にたまっていくことがないので、絶縁物試料を用いてもチャージアップが 起こりません。このため、低加速電圧SEMがSEM観察の主流になってきたのですが、 問題は空間分解能でした。電子顕微鏡の分解能は、加速電圧に大きく依存します ので、30kVから1kVに加速電圧を落とすと、ボケた像になります。空間分解能を 低加速電圧でも高いままで保つための方法として、リターディングという手法が 取られました[Frosien et. al. 1989]。リターディングは、高加速電圧で電子銃を 出た電子を試料の直前で減速させて1~2kVの低加速電圧で試料にあてるものです。 リターディングをさせるとどうして分解能が上がるかの説明は、ウィーンフィルタ の話ではないので省略しますが、このリターディングによって、二次電子に大きな 影響がありました。 二次電子は試料から出たときは数ボルトの低加速であり、出たとたんに強い磁場に さらされる点は前と同じですが、同時に強い電場にもさらされることになります。 一次ビームに対して減速場となる電圧は、反対方向を向いて進む二次電子に対しては 加速場になります。つまり、1Vで試料から出た二次電子は、対物レンズの中を通って いる間に30kVまで加速されるのです。対物レンズの上に置かれたウィーンフィルタに 達した時に二次電子は30kVの加速電圧になっています。ウィーンフィルタは30kVの ビームを90°曲げるだけの強さに電場と磁場を設定しなければなりません。 ここで、今までとは全く違う事情が起こります。それは、ウィーンフィルタの電場磁場 が強くなったためこれが一次ビームの軌道に影響を与えるようになることです。一次 ビームがウィーンフィルタのフリンジ付近の電場分布と磁場分布の一致の問題や、 ウィーンフィルタの作る収差の問題が試料上のビームサイズに影響を与えるようになり 、ウィーンフィルタの詳しい解析が要求されるようになったのです。SEMの空間分解能 は、入射ビームのスポットサイズで決まりますが、ウィーンフィルタの収差は、直接 それに影響を及ぼします。そのため、ウィーンフィルタのビームセパレーターへの 応用に関する論文や特許がたくさん出されるようになりました[Takafuji et. al. 2000, Kienle & Plies 2004]。この問題はまだ完全には解決しているとは言えず、 現在も研究が行われています。 6.スピン回転器への応用ウィーンフィルタはフィルタと言う名前で呼ばれているにもかかわらず、フィルタ、 即ちエネルギー選別の道具としてだけではなく、別の用途にも使うことが出来ます。 上で説明したビームセパレータもその一つの応用ではありましたが、それでも ローレンツ力を利用した装置であるという点では、電子レンズ、電子線エネルギー アナライザと同種の装置であると言えます。ところが、ここでご紹介するスピン 回転器は、電子に対する磁場のローレンツ力を利用したものではなく、磁場がスピン に直接作用する力を利用したものです。電場は何のために使われるかと言いますと、 それは磁場によるローレンツ力をキャンセルし、ビームを直進させるのが目的に なります。つまり、ローレンツ力はこの応用にとってはむしろ邪魔になるわけです。 ただ、ビームセパレータの場合と同じように、スピン回転器もセクター磁石と円筒 電極の組み合わせで、90°偏向でも使われています。これは初期の歴史の項で説明 した、ウィーンフィルタ初期1930年代の質量分析装置に使われたことのあるものと 同じ構造です。ウィーンフィルタの場合は、ビームが直進しますが、セクター磁石を 使った場合は90°回転した方向にビームが出てきます。スピン回転器をつなげた電子 ビーム機器で、直進の方が便利な場合は、ウィーンフィルタを使い、90°曲げると 装置全体が都合よく収まる場合は90°偏向器が選ばれているようです。ウィーンフィルタは電子レンズの間に挟んで使います。最初の電子レンズで、 ウィーンフィルタの中心にフォーカスするようにビームを入れます。こうすると、 ウィーンフィルタの電場磁場の大きさを変えても全体のレンズ作用はあまり変化 しなくなります。と言ってもウィーンフィルタがある程度の長さがあるので、強さに よって多少のレンズ作用が変化しますので、それは後ろの電子レンズで戻してやり ます。こういう構成にすると、電子のスピン回転角は磁場の強さだけで決まります ので、それほどレンズ作用を変えずにスピンの回転角度だけを変化させることが 出来ます。電場は磁場の大きさに対して、ウィーン条件E1=vB1に従って、B1の変化 に比例してE1の大きさを変えてやることでビームを直進させる役割を負うことに なります。これがウィーンフィルタを利用したスピン回転器の仕組みです。 スピン回転器は、スピンSEMと呼ばれる磁区観察装置として実用化されています [Kohashi et. al. 2004, 2010]。スピンSEMは、試料の磁区構造に従って出てくる 二次電子のスピンの向きが影響を受けるが、あらかじめスピン偏極をした電子 ビームを試料にあて、入射ビームと試料の磁区の中のスピンの方向によって反射 電子の放出量に差が出ることを利用したSpinLEEMにも利用されています [Suzuki et. al.2009]。 7.ウィーンフィルタを利用したフェイズシフターへの応用電子は粒子であるとともに波でもあります。今までの話はすべて電子の粒子としての 性質に関係した事柄でしたが、波としての電子の性質をコントロールすることにも ウィーンフィルタは応用されています。この応用を行ったのはドイツのチュービンゲ ン大学のHaselbackです[Hasselbach 1997]。チュービンゲン大学は、電子ビーム研究の 元祖であるドイツの中でもその中心をなす大学で、美しい小さな大学町に多くの電子 ビーム研究者がいました。ホログラフィーと言うのは普通の光で広く使われていますが、電子ビームを使った ホログラフィーの研究もおこなわれています。電子線ホログラフィーでは日立の外村 さんが有名ですが2012年の5月にお亡くなりになりました。ドイツではLichteが盛んに 研究しています。このホログラフィーと言うのは、バイプリズムと言って、細い導電性 の線に電圧をかけ、電子ビームを当てると、ビームは二つに分裂します。このうちの 片方を試料にあて、もう片方を真空中に通します。その後再び二つのビームを交わら せて干渉縞を作ったのがホログラフィーで普通には検出器に記録することのできない 波の位相情報を記録することが出来ます。この流れの中で、ウィーンフィルタは どこに使えるかと言いますと、二本に分かれたビームの一方は物質中を通り、他方は 真空中を通るため、両者の間に位相のずれを生じます。両者をウィーンフィルタ の中を通すと、プラス極に近い方のビームの位相を進めてやることが出来、もう 一方のマイナス極に近いほうのビームの位相を遅らせることができます。このように して二つに分かれたビームの位相のずれをお互いに調節することで干渉性を良くして やることが出来ます。 8.ウィーンフィルタの収差補正への応用Schelzerの定理[Schelzer 1936]と呼ばれているいくつかの球面収差係数Csや 色収差係数Ccが正の値を取って負にすることが出来ない条件の中に、軸対称な 電場と磁場と言う項目があります。この項目が収差補正の分野では最も良く 知られている項であり、それによって現在盛んに使われている多極子を利用した 収差補正器が開発されています。ところが、この項は誤解して理解されている場合 が多いようです。誤解はこの定理を軸対称なレンズと解釈することです。軸対称場 と軸対称レンズはどう異なるかと言いますと、非対称な場からも軸対称なレンズを 作ることが出来るからです。すなわち、多極場を用いていながら軸対称なレンズを 作ることによって、シェルツァーの定理に矛盾せずに負の収差を作ることが出来る のがウィーンフィルタなのです。非対象レンズの場合は収差補正を行うのに何段も の多極子やラウンドレンズを組み合わせた複雑な系を構成する必要がありますが、 軸対象レンズの場合は、一個のレンズで行うことができます。もうひとつ軸対称 レンズでありながら負の収差が作れるのが静電ミラーでありますが、この場合も 二段ないしは三段の電極構成をしたミラー一個で負の収差を作り出しています。 シェルツァーの論文はドイツ語で書かれているため私を含め多くの人は実際には 読んでいないのではないかと思われます。色々な人がシェルツァーの定理はこれだ と述べていますが、それぞれ微妙に違っています。 それでは、ウィーンフィルタによってどのようにして収差補正が出来るのでしょうか [Ioanoviciu et. al. 2004, Tsuno et. al. 2005]。まず、色収差Ccに付いて考えて みましょう。ウィーンフィルタは一様な電場と一様な磁場に電場または磁場の4極場 を重畳した場の組み合わせで、非点なし結像を行わせます。このときのビームは、 ラウンドレンズ収束と言う普通の軸対称レンズと同じ、軸対称な軌道を描きます。 軸対称レンズと違う点は、X方向に分散を生ずることと、2次の収差を発生すること です。軸対称レンズは二次の収差は対称性によって作られず、一次の色収差の他は 3次の収差から始まります。 しかし、これはウィーンフィルタに限らずすべてのアナライザに共通したことですが、 二回フォーカスを行わせると、分散と二次の幾何収差が消滅します。そこで、ウィーン フィルタで収差補正を行う場合も二回フォーカスで取り組むことになります。 エネルギーアナライザのように分散を利用するわけではないので、一回フォーカスを した後にスリットを入れる必要はありません。こうして二回フォーカスをさせた ウィーンフィルタで残るのは二次の色収差です。ここで二次の色収差と言っている のは実は軸上色収差Ccを含むビームの角度に対して一次の色収差のことで、この 角度とビームのエネルギーの変化分δVをかけて二次と呼んでいます。この混乱は、 収差を表現する理論がいくつかあり、ここではマトリックス法と呼ばれる加速器や 質量分析装置で主に使われている理論で呼ばれている名前を使っているため、電子 顕微鏡で使われている収差の標識と若干異なった呼び方がされているせいです。 この二次の色収差をキャンセルするための条件は、実はウィーンフィルターの理論 から明らかになっており、電場の4極子成分と、磁場の4極子成分を両方反対向きに お互いにキャンセルし合うようにかけておき、電場の4極子成分が磁場より多く かかっていて非点なし結像を達成できる条件にしておきます。こうした条件の もとで、さらに6極成分をかけます。6極子は二次の色収差のキャンセルには電場 でも磁場でも良く、両者の差が一定の値を持てば良いような関係でかけます。 こうした条件で、4極子と6極子をかけると、二次の色収差が消えて、二次まで の収差に関しては、Ccだけが残ります。Ccに色々の値を取らせるためには、4極子 と6極子の条件を上に述べたように保ったまま4極子の大きさを色々に変えてやる ことで実現します。このようにして、Cc補正の条件が決まります。しかし、実際 には、この時3次の収差も発生するので、Ccだけを補正するためには、3次の収差 を零にする条件に設定しておいた方が望ましいのですが、それは次のCs補正の所で 述べます。他の収差補正法では、Cc補正装置でCs=0の条件で使うなどと言うことは していません。Cc補正をしようと思ったら出てきたCsは他の方法で補正すると言う のが一般的です。 次に、3次の収差である球面収差係数Csの補正はどのようにして行われるのかを見て みましょう。図12は、ダブルフォーカスウィーンフィルタの三次の収差を丸くする 条件を示しています。二次収差までの範囲では6極子場は、e3-b3の値が指定される だけで、e3とb3の値が指定されることはありませんでしたが、3次収差を規定しよう とすると、b3 = e22/9という値に固定されます。もちろん、e2-b2=-1/4という条件は ここでも生きています。さらに8極子項がe4-b4 = - 29e22/72という形で与えられます。 3次収差に関しては、8極子の電場と磁場の間には自由度があってその差が規定される だけです。 ウィーンフィルタの開口収差(球面収差Csを含む軸対称な3次収差)が零になる条件は、 4e22 + 12e2 + 3 = 0. という二次方程式で書くことができます。二次方程式であるからその解は二個あって、 4e2 = -10.8990 と -1.1010 です。後の方の近くで収差図形をフォーカスを少し だけ変えて、またe2の値も少しずつ変えて示したのが図13です。丁度4e2=-1.1010に 等しくなったフォーカス位置で開口収差は零となっています。すなわち、零がある ということはその前後で符号の変化があり、マイナスの収差を示す条件があるという ことです。 図13に横軸に4極子電場e2の値をとり、縦軸にCsとCcの変化を示しました。Ccはe2に 対して直線関係にあり、Csはe2に対して二次方程式の関係にありますので放物線を 示しています。e2の値はサイクロトロン半径Rによって変化するのでCsとCcの間の 関係はフィルター長Lを変えることによって変化させることは出来ますが、長すぎる あるいは短すぎるフィルタを作ることには困難があり、Lの実用的範囲は10mmから 100mmの間であり、電極間に放電なしで印加できる電場の強さも電極間距離が1mm弱 程度であることを考えると5kV以下にとらざるを得ません。このように考えると、 Lの範囲もおのずともっと狭い範囲に制約される可能性が高いことから、CsとCcの 関係を自由に取ることにおのずと制限がつきます。このことが、同じ軸対称な電子 軌道をとらせることのできるミラー型収差補正器と比較した場合のウィーン型収差 補正器の欠点となります。ただし、ミラー型の場合は、ビームセパレーターという 軸非対称性分をどうしても必要とする欠点がありますので、LEEM/PEEMや低加速電圧 SEMといった分野では、Wien型補正器に分がある場合も考えられます。 9.q-レンズによる電子のスピン軌道角運動量への作用と色収差補正への応用ウィーンフィルタは、電場と磁場を重畳し、それぞれの場によるビームの偏向作用を 打ち消し合わせるものです。この作用は一様場E1, B1に限るものではありません。 4極場E2, B2でも同様にウィーン条件を満たせばそれぞれの場によるレンズ作用を キャンセルさせることが出来ます。一様場の場合は、レンズ作用をキャンセルさせる ことは出来ませんでした。キャンセル出来たのは偏向作用だけです。レンズ作用は両方 の場ともに電場方向即ちX方向に働き、磁場方向即ちY方向には何の作用もありません。 従って、これらを重畳してもレンズ作用をキャンセルすることはできません。 こうした状況を実現すると、電子に対して4極場の作用によるローレンツ力以外の効果を 及ぼすことが出来ます。電子には、電荷の他に、スピンと、軌道角運動量という性質が あります。スピンにらせん運動をする軌道角運動量を持たせておくと、それをウィーン フィルタの4極場を通したときに電子の持つスピンの向きを整列させるという働きがあり ませんが、とにかく、ウィーン条件を一様場だけでなく4極場にも適用できること、そして、 軌道角運動量と言った電子の別の性質に対して作用させる素子として利用できるのです。 おわりにこのようにウィーンフィルタはひとりエネルギーアナライザという分析装置としてだけでは なく、荷電粒子のいろいろな性質に働きかける素子として幅広い応用が広がっています。 分析装置としてではなく、電子の電荷と質量の比を測定する装置として発明されたウィーン フィルタは長い空白の時を超えて蘇り、同じ時期に発見されたX線同様に幅広い分野に応用 される装置になっています。図13に見られるように、両条件が満たされたときにだけ、 ビームが丸くなっています。 図8に示した形状が、非点なしフォーカスを実現し、かつフリンジにおいてもWien条件を ある程度満たすことのできるWien Filterの一つの到達点を示しています。そこに至るまで、 私が試行錯誤して、これまでに制作したあるいは考えたWien Filterの形状を図21から図23 までに示します。最初は、非点なしフォーカスが実現できる断面形状を持つふぃたを設計し ました(図21)。この形状は、Sheinfeinによって、提案されていました。しかし、これでは 電場の一様性が取れなかったため、図22に示す一様電場・一様磁場を実現する形状(図22) へと進み、さらには、図23において、一様電場・傾斜磁場の生成に成功しました。しかし、 この段階までは、フリンジ場におけるWien条件成立の手立ては何も行っておりません でした。フリンジ場においてもWien条件が成立する形状は、図8に示したものによって、 実現しました。 コンタクト・質問は、こちらまで ♪EOS津野"eostsuno@yahoo.co.jp" 作成日 2017/12/04 改正2018/11/23 2019/01/09, 2019/04/24 |
|