|
EOS津野の 電子光学講座 Contact: eostsuno@yahoo.co.jp |
タングステンヘアピンフィラメントは、透過型や走査型と言った電子顕微鏡の主として汎用機に今でも
用いられています。フィラメントに覆いかぶさるようにウェネルトと呼ばれる電極
があり、負の電圧が掛けられています。ウェネルトの目的は、フィラメントを加熱
した時にタングステン線材のいたるところから熱電子が発生すると、真空中に出てきた電子が
フィラメントの近くに漂ってしまい、これらの電子は
負の極性を持っているために次に出てこようとする熱電子を抑制する働きをしてしまうと言う
ことでした。このような、熱電子の抑制効果を空間電荷効果と呼ぶのだと
教わりました。ウェネルトはこの効果を防ぐためにウェネルトによって開発されたもので、
負の電圧をかけることによって、穴の付近のフィラメント先端以外の場所から熱電子が出てくることを
抑制し、電子は先端だけから出てくるようにしたというわけです。
近年、光電子分光などでより高いエネルギー分解能が求められるようになりますと、半球フィルタなどに 入射させる電子の加速電圧がどんどん低くなり、数ボルト程度が用いられるようになって います。こうした低い加速電圧でレンズやエネルギーアナライザを使う場合、再び空間電荷効果が 効いてくる可能性があると言われています。もちろん、空間電荷効果が効くかどうかは、加速 電圧だけではなく、電流量にも依存します。SEMのようにピコアンペアの電流でも像を作ることが出来る 装置では、例え電圧が数十ボルトと低くても空間電荷効果とは無縁かもしれません。しかし、分析装置 などでは、大きな電流を必要とする場合が多いようです。この場合、装置の設計には空間電荷の考慮が 必要になるのではないかと思われます。ここでは、空間電荷効果を入れた軌道計算によって電子軌道 にどのような影響が出るかを調べてみることにします。 |
空間電荷効果を考慮した静電レンズの軌道計算1. リターディング電極を持つアインツェルレンズ系ここでは、空間電荷効果(Space Charge)を考慮した場合に静電レンズの電子軌道がどのように 変化するかを調べます。対象としたレンズ系を図1に示します。左側から100Vの加速電圧で 入ってきた色々な電流の電子ビームが左側のアインツェルレンズ(3極構成)でその次の 減速レンズ(2極構成)の中心付近にビームをフォーカスさせます。減速レンズでは、100V で入ってきた電子ビームを10Vにまで減速して右側の電極から出してやります。減速レンズ は一般的に収差が大変大きいため、ここでフォーカスを作ることによって収差を最小限に します。減速レンズから出てきた電子ビームを次のアインツェルレンズで受けて、右端 近くにある試料上にフォーカスします。このような系にすれば、加速電圧が100Vの領域と10Vの領域が二通り出来ますので、 Space Charge空間電荷効果の効き方の加速電圧による違いを見ることが出来ます。 図2は、1nAの電子ビームを入れた場合の電子軌道です。上に述べた軌道を作るために 必要とされた各電極の電圧は図の上に示してあります。減速レンズは2電極ありますが、 右側の電極は-90Vに置かれています。これは、左側から-100Vに加速された電子が アース電位にあるアインツェルレンズに向かって100Vの加速電圧で入ってきたためです。 これで、加速電圧は-100V-(-90V)=-10Vとなって、加速電圧-10Vのビームとなります。 ただ、この減速電極より右側の電極と試料は全て-90Vの電圧上に置かれることになります。右側の アインツェルレンズの真ん中の極はこの-90Vにさらに、ビームをフォーカスさせるに必要な 電圧が加算されているわけです。 このような構成にしますと、試料を-90Vの電圧上に置かなければなりませんので、何かと 不便になります。これを防ぐためには、全体の系に+90Vを足してやります。そうしますと、今 図2で-90Vと書かれた電極全てが0V即ちアース電位に置かれることになります。最初に入射する ビームの電圧は-10Vです。一番左側のアインツェルレンズの電極は、0V+90V=90Vで+90Vの電圧 上に載ることになります。つまり、電子は-10Vから+90Vに向かって加速電圧100Vで加速される ことになります。このように実際の装置では実験のやりやすさに、費用の少なさなどを基準 にして、どこにアース電位を置くか決められます。 電流を増していった時の空間電荷効果による軌道の変化さて、それでは電子ビームの電流値を増すことによって電子の軌道にどのような変化を生ずるかを 次に見てみましょう。図3は図2に示した1nAの電流から電流値を一桁ずつ増して行った場合の 電子軌道の変化を示しています。10nAではこの図で見る限りほとんど変化は見られません。しかし、 100nAに電流が増えた所で加速電圧が10Vに減速されてからの軌道でフォーカス位置が右側に ずれていることが分かります。これは、空間電荷が影響を及ぼし始めて、凹レンズの作用をしたことが わかります。収差補正の理論で有名な シェルツァーの定理に、軸対称な電子レンズが正の収差しか 持てない場合の範囲を示した中に、空間電荷を持たないことと言う但し書きがあったことを 覚えています。逆に言えば、空間電荷は凹レンズを作り、その結果、負の収差係数を示すこともある と言うことだと言うことがこの図から納得がいきます。空間電荷の影響を計算したの文献は 数は少ないですがあります(文献1)。 しかし、空間電荷はそれが効き始めた時には凹レンズを示すと言うことは面白いことだと思います。 もちろん、電子同士が反発しあう結果ですから、発散方向に電子が向かうのは当然と言えば当然 のことではあります。更に電流を増やして1μAになりますと、ビームは大きく広がってしまい、レンズ作用どころでは なくなります。レンズ作用としては凹レンズだと言うことは、ビームが発散していますので良く わかります。一方、リターディング電極の中でのフォーカス位置について見てみますと、100nA のビームの場合と比べて、フォーカス位置が右側にずれていることが分かります。空間電荷の 影響が顕著になってきたということを表わしています。そして、ビーム電流が10μAにまで 増えますと、もはや加速電圧100Vから10Vへの減速領域でもビームが大きく広がってしまっ ていることが分かります。 このように電流値を増していくにつれ、まずフォーカス位置の遅れが生じ、次にビームの広がり が起こると言うことが空間電荷効果の現れ方であることが分かります。 収差について図4では、収束位置での軌道を10nAのビームと100nAのビームとで比較しています。ビームの角度は 3種類取っています。角度の大きいビームほど早く(左側で)収束しています。その大きさは 全体として一番ビームが細くなった面即ち、最小錯乱円の位置で5倍ほど違っているように見えますが、 Z=70mmの位置で比較したスポット形状を図5に示していますが、この位置では2倍ほどになっています。このように空間電荷の影響はシミュレーションによってきれいに示すことが出来ますが、その方法は 磁場レンズの場合に磁気飽和の影響を計算する時の方法と似ています。磁気飽和を計算する時には、 最初は磁極の各位置での磁束密度が分かりませんので、磁化曲線データーの最初の値を使って、そ の磁束密度での透磁率を用いて磁束密度を計算します。この時は、磁気飽和のない時の透磁率が 用いられますので、高い磁束密度が得られます。次に、得られた磁束密度に対応する透磁率を使って 計算をやり直しますが、この時は最初に高い磁束密度が得られていますので、それに対応する透磁率 は低い値になってしまいます。そこで二度目の計算では、得られた磁場の値は低くなってしまいます。 3°目の計算では、低い磁場に対応する透磁率を使いますので高い透磁率になって強い磁場が得られます。 このようにして繰り返し計算をすることによって、正しい値に近付けて行きます。この手法はニュートン・ ラフソン法と呼ばれていました。空間電荷効果の計算でも同じように最初は、空間電荷のない場合の電場 に対する軌道を求めます。得られた軌道が作る電場を次に求め、レンズの場との合成の電場分布を 出力します。2番目の計算で、この合成の電場を使って軌道計算を行いますが、最初に空間電荷のない 場合の軌道を求めていますので、その軌道にある電子の作る電場を考慮すると大きな空間電荷になっ てしまい、電子が通らなかったりすることになります。二番目は、大きな空間電荷の影響のもとでの 軌道計算になりますので、電子の通りが悪くなり、今度は空間電荷の小さな結果になります。3番目 4番目と計算するうちに収束していく点は磁気飽和の影響の計算と同じです。磁気飽和の計算と 空間電荷の影響の計算で大きく違うのは、磁場の場合には、磁場計算だけで閉じていますが、空間電荷の 計算の場合には、電場の計算だけではなく、電子の軌道計算をして初めて空間電荷が計算できます。 そういう意味で、空間電荷計算の方が高級と言いますか、込み入った計算が必要になります。 コンタクト・質問は、こちらまで♪ EOS津野"eostsuno@yahoo.co.jp" 著者のページ 作成日 2017/08/15 2018/11/21 |
|
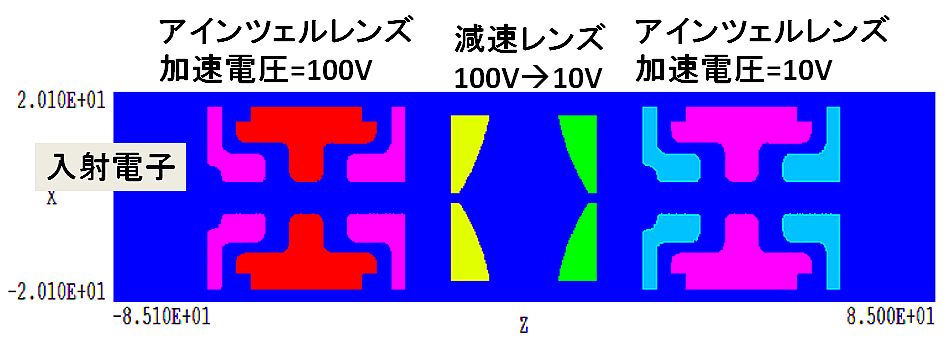 図1.低い加速電圧のレンズ系でSpace Chargeの影響を調べるアインツェルレンズと減速レンズを含む
電子光学系。
図1.低い加速電圧のレンズ系でSpace Chargeの影響を調べるアインツェルレンズと減速レンズを含む
電子光学系。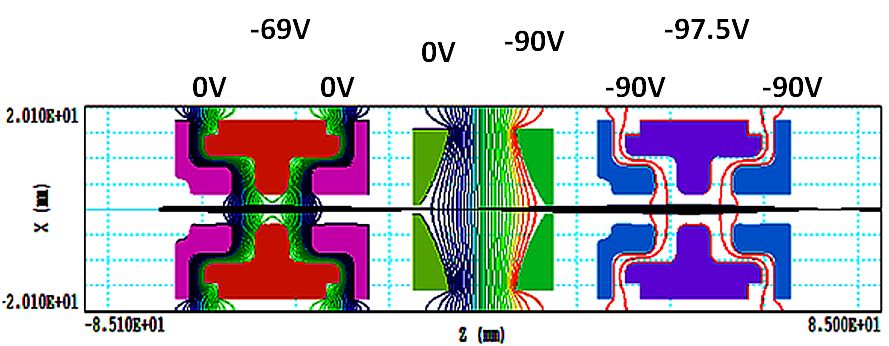 図2.図1のレンズ系に入射した電流値1nAの電子ビーム軌道。
図2.図1のレンズ系に入射した電流値1nAの電子ビーム軌道。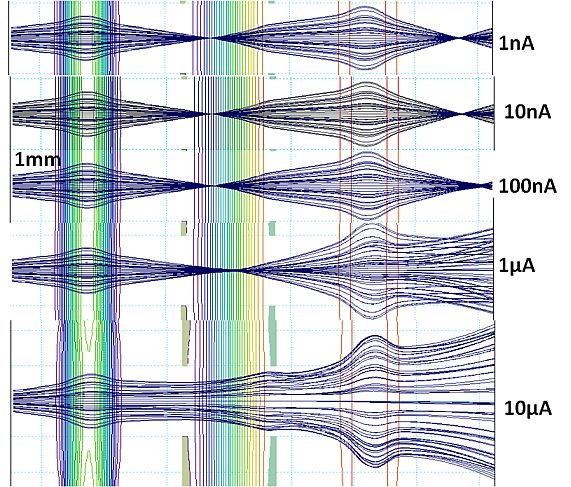 図3.入射電流を1nAから10μAまで変化させた時の空間電荷効果による電子ビームの軌道の変化。
図3.入射電流を1nAから10μAまで変化させた時の空間電荷効果による電子ビームの軌道の変化。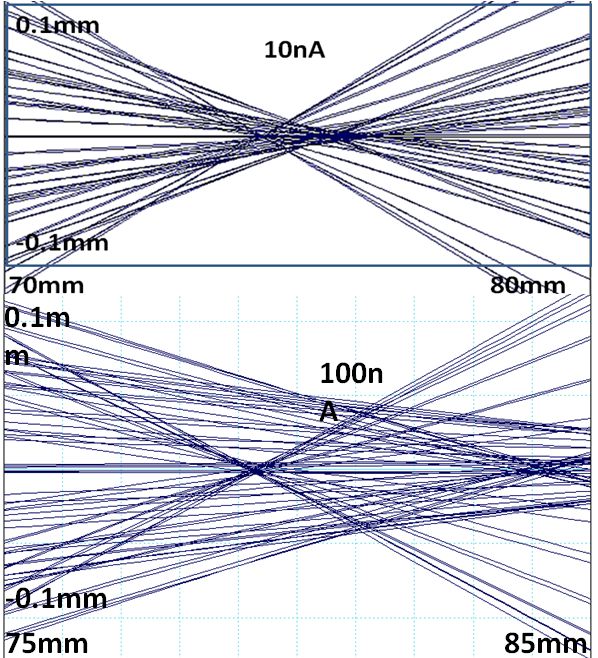 図4. ビーム電流10nAと、100nAの場合のビーム収束位置での軌道の比較。
図4. ビーム電流10nAと、100nAの場合のビーム収束位置での軌道の比較。 図5. 10nAと100nAビームのZ=170mm位置でのビーム形状。
図5. 10nAと100nAビームのZ=170mm位置でのビーム形状。