8極子を使った静電偏向器
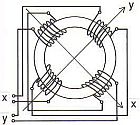
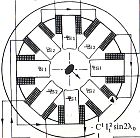
図1に8極子を使った静電偏向器の3D図面を示します。また、図2には、XY面の断面図を各電極
に与える電圧と共に示しています。ここで、VxはX方向の電場を作るための電圧、VyはY方向の
それを表します。今、X方向の電圧についてだけ見てみることにしましょう。左側が-Vx、右側
が+Vxになっていますが、ギャップも含めて考えると、それぞれ180°ずつを占めていますから、
前のページで調べた、一様場を得るための角度120°をはるかに超えています。しかし、上下の
電圧を見てみますと、+-Vxではなく、+-bVxと書かれています。この係数bを0から1までのいろ
いろな値を入れて、電場分布を調べたグラフが裏先生の本「ナノ電子光学」(共立出版2005年)
のp.146に出ています。それによると、b=root(2)-1=0.4142の時に電場が一様になることが示
されています。
同じ形の電極を8本並べた多極子で、X方向に一様な電場を作るときには、横方向の4本の電極に
+-Vxを与えたとしたら、上下方向の4本の電極には+-0.41Vxの電場を与えれば良いということが
わかりました。いま、図2で黒い字で示したX方向の場合について述べましたが、まったく同じ
ことは赤い字で書いたY方向の電場についても言えます。そこで、X方向とY方向にそれぞれ好きな
電場を作り、その合計の電圧を各電極に与えれば、任意の方向に任意の大きさの電場を作ること
ができることがわかります。ただ、図からわかりますように、8個の電極に与えられる電圧は
すべて異なる値となりますから、電源は8個必要になります。前ページで説明した2段偏向を
行おうとすれば、その2倍、すなわち16台の電源が必要になるわけです。
さて、これまではX方向の電場とY方向の電場について独立に求め、それらを合成すると、ベク
トル和の方向に電場ができるという考え方をしてきました。しかしながら、実はもう一つもっと
簡単な理解の仕方もあります。それは、電場の方向はコサイン関数で表されるという考え方です。
図2の電極は、水平線の右側から反時計回りに数えて、22.5°67.5°、112.5°、157.5°、202.5°、
247.5°、292.5°、337.5°の8方向に向いた極があります。このコサインを取りますと、0.9239,
0.3827, -0.3827, -0.9239, -0.9239, -0.3827, 0.3827, 0.9239となります。0.3827/0.9239=0.4142
ですから、0.9239V1の電圧をV1とした場合には、0.3827V1の極の電圧は0.4142となりますから、
上の場合と同じ比率であることがわかります。
このようにコサインで考えると、係数bの値がいくらになるかわざわざ実験したり、シミュレー
ションをしなくてもいくらの値を用いればよいかがわかります。さらに便利なのは、このコサ
イン則は8極子だけに適用されるわけではなく、何極の場合でも、各極の大きさが一様でない場
合にも使うことができる一般的な規則です。
コサインの法則でさらに便利なのは、電場の向きを回転させるのに、Cos(θ+α)として各極に
与える係数を計算すればよいことです。ここで、θは各極の方向、αが電場の回転角になります。
電子顕微鏡の偏向器などはすべて、X, Yで表示されていますが、向きαと強度Iで表すことも
できるわけです。
偏向器と非点補正器のトップに戻る
|
図1.静電8極子の3D表示 |
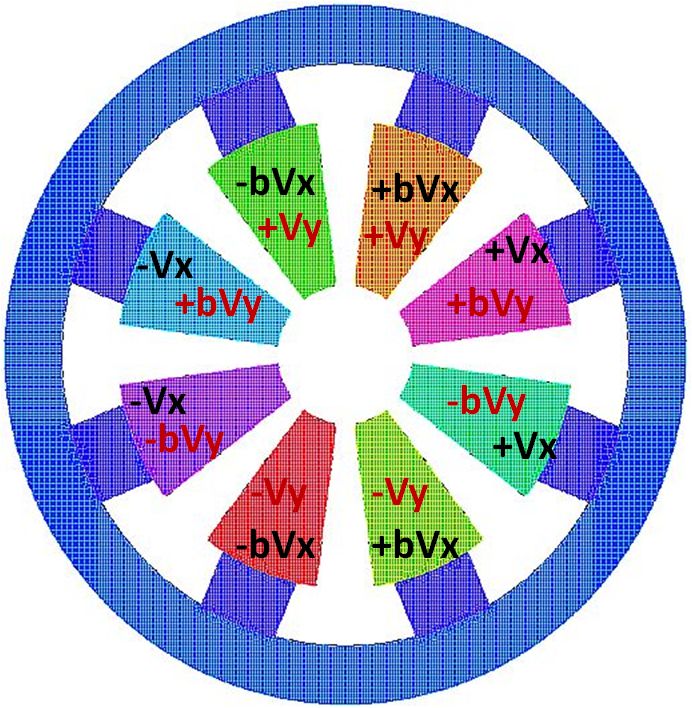図2. 静電8極子のXY断面 |
|
S.jpg)
S.jpg)
