|
EOS津野の 電子光学講座 Contact: eostsuno@yahoo.co.jp |
STYLE
コンピューターシミュレーション法の典型的応用の一つである有限要素法を電磁界計算、特に 電子顕微鏡のレンズ設計に応用したのが、イギリスはケンブリッジ大学のドクターコースの学生 だったDr.Munroでした。彼のソフトはケンブリッジ大学図書館より無償で配布されており、それを 理研で手に入れたものをコピーさせてもらったのが、J社でソフトを入手した方法でした。Munro 博士は、ロンドンのインペリアルカレッジに就職し、1984年ころは、アメリカのオレゴン大学に 留学していました。帰ってからしばらくして、お弟子さんだったDr. Rouseさんと一緒に会社を立ち 上げソフトの種類も増やして、ソフトの製作と販売に専念することになりました。ここでは、 このDr.Munroソフトによるレンズ設計法の導入時代のお話しをします。 |
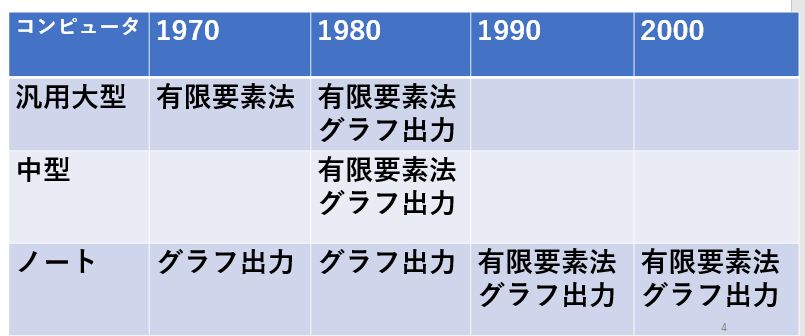
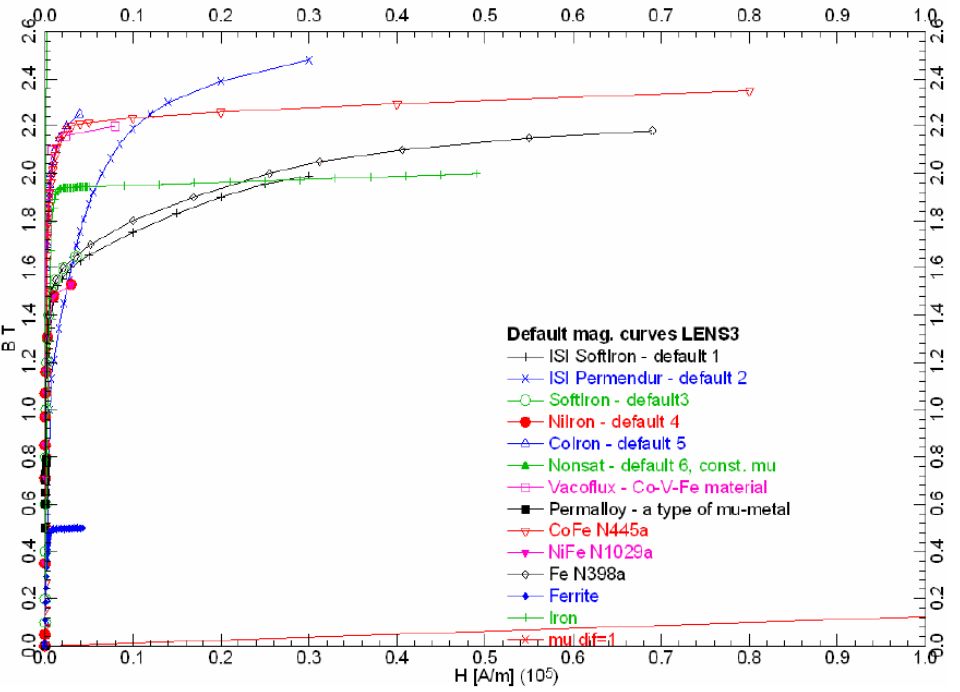
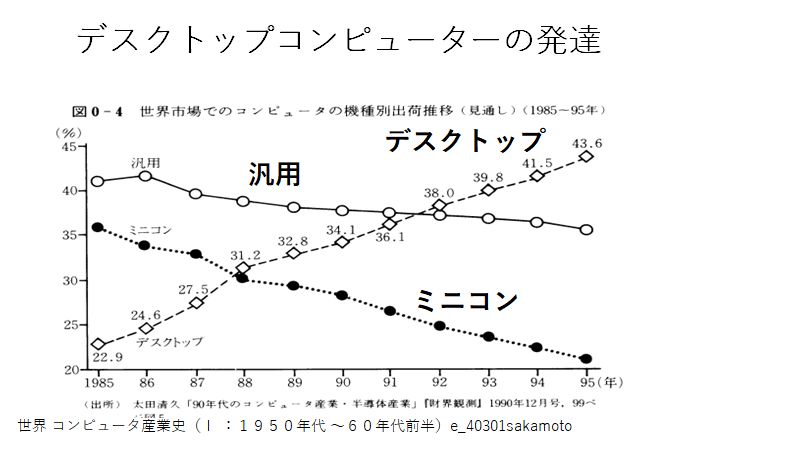
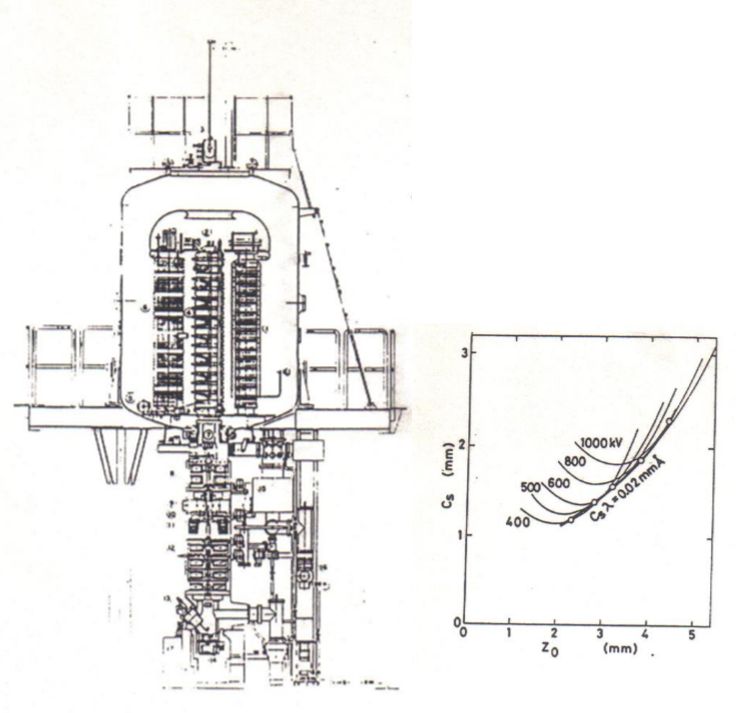
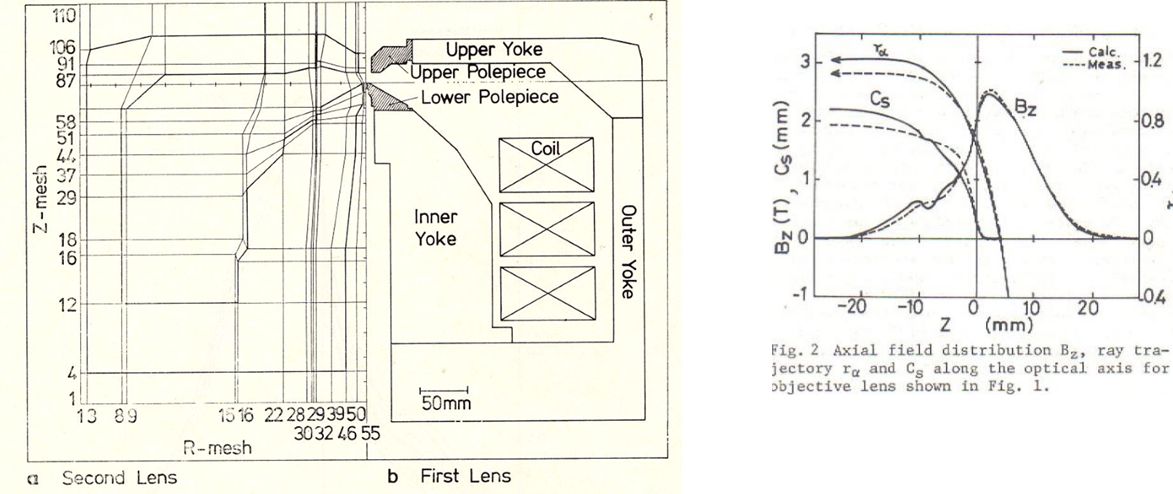
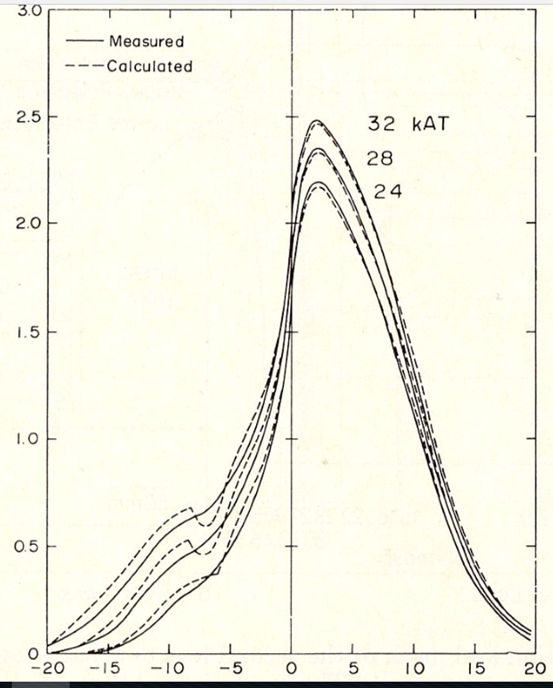
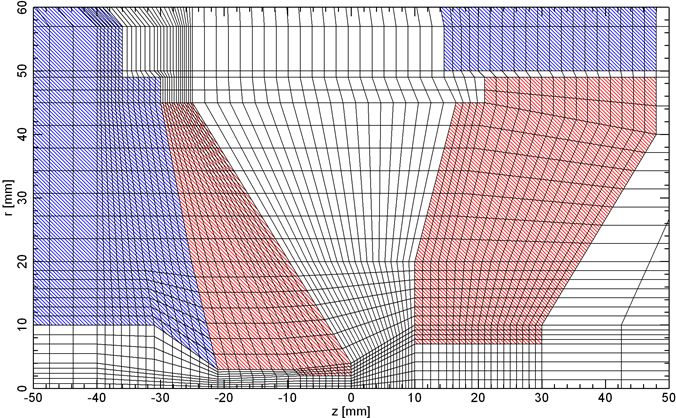
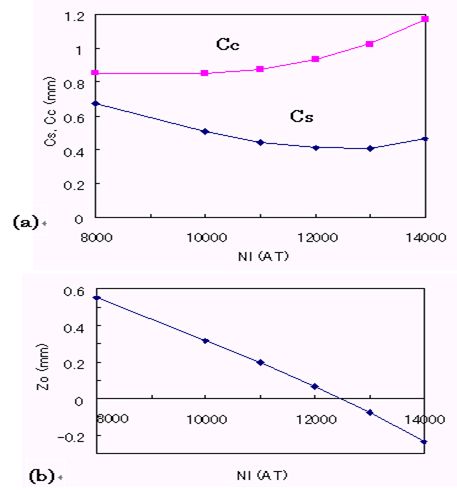
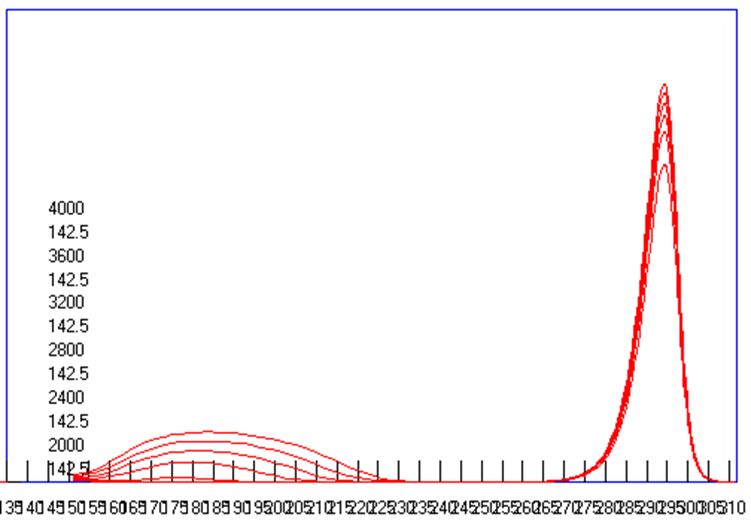
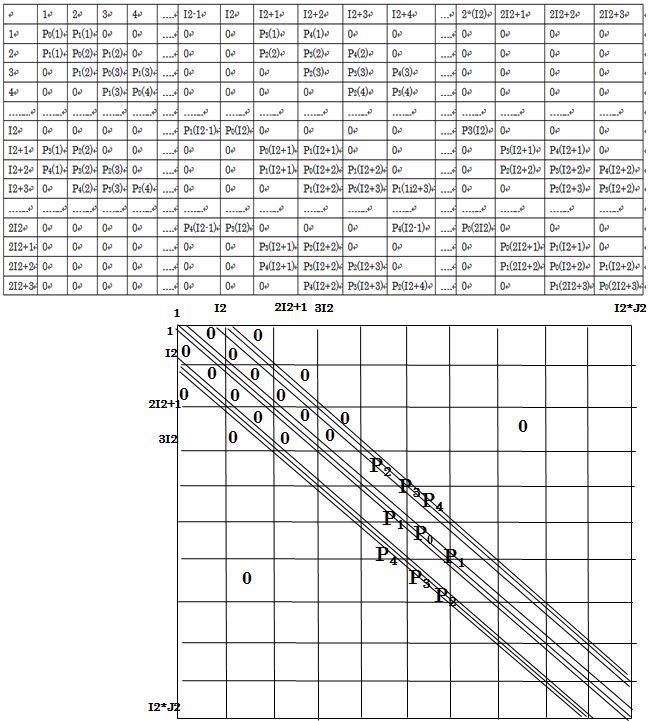
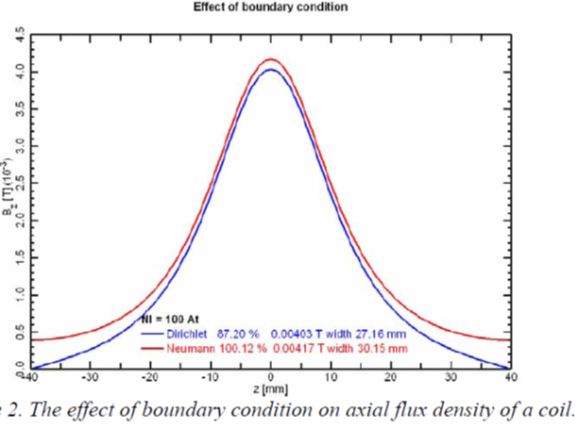
<--レンズ設計のためのMunroソフト --電子顕微鏡のレンズ設計は神の手によってなされるものと言われ、それが出来るのはごく限られた 人だけで、厳しく選択された師弟関係によってのみ伝えられておりました。1980年代に入って間も なく、丁度1000kV超高圧電子顕微鏡の商談が3件: 北大、東工大、アメリカのUCバークレーより あり、北大と東工大をH社、バークレーのみをJ社で受注いたしました。バークレーの1000kV機は、これまで製作して来た同種の装置と比べ、より高いスペックを要求 されていましたので、新たな設計を必要としました。この頃、納入済みの1000kV機のうち、東北 大より、磁区観察用の磁場フリー型レンズを受注しており、その納入に際し、そのレンズの軸上 磁場分布の測定が義務ずけられてれておりました。そこで、磁区観察ポールピースの納入に際して 、磁場測定用ガウスメーターを車に積んで、東北大を訪問し、同時に、高分解能用レンズの軸上 磁場分布も測定して帰りました。 200kV用レンズの場合、高空間分解能用レンズの軸上磁場分布は、レンズの孔の直径が 磁場測定用ガウスメーターのプローブ径より小さかったため、測定したことがありま せんでしたが、1000kV機の場合、穴の直径がプローブ径よりも大きかったため、測定し て帰ることが出来ました。 戻ってから、この当時すでに社内に導入されていたMunroソフト即ち有限要素法 を利用した、電子顕微鏡レンズの磁場分布、その中心軸上を走る電子の軌道と、収差の 計算ソフトソフトを使って、会社に残っていた東北大向け超高圧電子顕微鏡の磁場分布 の計算を行い、実験で得られた分布と比較しました。Munroソフトの導入は当時 半導体部門で、リソグラフィー装置や半導体検査装置で付き合いのあった理化学研究所 経由で行われていました(図1)。当時は、Munroソフトはケンブリッジ大学図書館から 無償で公開されていました。 結果は無残なもので、磁場の値が強く出すぎていました。可能な範囲で、有限要素メッシュ の分割数を変えて、何種類かのデータを作って結果を比べてみますと、メッシュ間隔を細か くするほど、つまりコンピューターのメモリーを沢山使う計算をするほど磁場の値は小さく なることが分かりました。社内の汎用コンピューターではメッシュ数を増やしていったときに 磁場の値が一定値に近づくようなレベルではありませんでした。もっと大きなメモリー数を 使わなければ到底役に立つような計算結果が得られる水準ではありませんでした。 そこで、入力データーだけを何種類かパンチカード(図2)で作り、外部に依頼して計算する ことでこれ以上メッシュ数を増やしても磁場の値がほとんど変わらない数のメッシュを調べ、 それを計算出来るコンピューターを備えている研究所に委託して計算をすることにしました。 しかしながら、一定値に落ち着いた後でも、計算値は実験値より良い値に留まっていました。 そこで、これは磁化曲線(図3)の問題として扱うしかないと考え、磁化曲線にある数値をかけて、 特性を少しだけ悪くすることによって、実験値と計算値がほぼ一致するように調整しました。 と言うのも、鉄コバルト合金の磁化曲線は、熱処理条件に敏感で、外形45mm, 内径33mmの いわゆるJISリングでは熱処理条件が実際のレンズとはかなり違ってしまい、小さなリングの 磁化特性が大きなレンズの磁化特性より良く出てしまう可能性があると考えられたから でした。本来はレンズと同じ外形のリングを作り、なるべく同じ熱処理を施し、普通磁化曲線 測定に使うアンペアターンよりずっと大きな値まで、磁化特性を測定すべきでしたが、当時は その余裕がありませんでした。 有限要素計算の外部委託は、それほど長期間を必要とせず、間もなく導入された汎用大型 コンピューターでは、必要なメモリーを確保できましたが、汎用計算機を事務処理と共同 で使用しなければならなかったことから、夜間のバッチ処理に限定されたこと、出力が ラインプリンタによる文字出力だけだったため、数値で打ち出された値を手入力で、当時 使用が始まっていたベーシックソフトのパーソナルコンピューターに手入力で打ち 込むことによってグラフを作成しなければなりませんでした。 まもなく導入されたIBMコンピューターについては、IBMユーザー向けにIBMが解放している 共同利用コンピューターを昼に利用でき、しかもそこで提供されていた機械ではグラフ 出力のためのアタッチメントがついており、数値出力データーを手入力でベーシックパソコン にコピーする手間も不要となり、昼間好きなだけ使うことが出来るようになりました。 翌年には同じグラフィック出力用アタッチメントを社内でも購入することが出来、 昼でも使えるだけの能力のあるコンピューターも整備され、自由度が増しました。 ミニコンによる計算とグラフ出力、そして有限要素法自体の進歩コンピューターの進歩は、以下のように分類され、有限要素法が力学への応用に 始まって、電磁気学にまで広がっていったのは第3.5世代からのことでした。 第一世代 1940年代: 真空管コンピュータ。汎用コンピューター 第二世代 1950年代: トランジスタコンピュータ。 第三世代 1960年代: 集積回路。 OS、タイムシェアリング。多様な展開。 3.5世代。 1970年代:。集積回路、仮想記憶 DECから小型で安価なPDP-8。 第四世代 1980年代: マイクロプロセッサ。パーソナルコンピューター。 第五世代 現在:: 人工知能。 米国カリホルニア大学バークレー校向け1000kV超高圧電子顕微鏡レンズ設計この当時、3台の1000kV超高圧電子顕微鏡の商談があり、北大と東工大をH社が、米国 カルホルニア大学バークレイ校のみJ社で受注いたしました。この1000kV機が 実質的に最初のコンピュータ設計による対物レンズとなりました。コンピューター設計 の妥当性を確かめるために、実機の磁場分布の測定が必要でしたが、高分解能機 の対物レンズは穴径が小さく、1000kV機のみが測定可能な大きさの穴を持っておりました。 そこで、東北大の既納高分解能レンズについて磁場分布を測定し、シミュレーションと 比較して、正しい答えの得られる計算条件を求めることが出来たわけです。 結果をドイツ・ハンブルクでのICEMに発表し、神の手によってしかできないと言われた 電子レンズの設計が普通の人の手によって可能になったことを報告いたしました。 図5の左側の図がバークレーに納入されました1000kV機の外観図で、右側に試料位置を 変えて計算で求めた球面収差係数Csの変化を加速電圧を400kVから1000kVまで変え ながら示しています。Csの実測値に関しましては、その後200kV, 400kV, 1000kVの 高分解能機につきまして、いくつかの納入先の研究機関からそこでの実測値の報告を 頂きましたが、クレームとしていただいた実測値は一件もありませんでした。装置の 保証値としてカタログに記載した値そのものが得られた場合もありましたが、それとは 隔たった値をご報告いただいた場合もありましたが、いずれも保証値より良い値であり、 喜ばれこそすれ、クレームとして報告されることはありませんでした。と言うことで、 計算に使用する鉄コバルト合金の磁化曲線を実験値より少しだけ悪くして計算で使用 したことが結果的に、商売としては役に立ったものと考えております。 図6の左側はは使用した対物レンズの断面図で、右側に計算で求めた軸上磁場分布と 実測によって求めた磁場分布と球面収差係数Csと色収差係数Ccの積分の途中の値を 示しています。電子軌道は普通左から右に進むように書かなければならないのですが、 MunroのソフトはSEM用に作られているため、そのままTEMに使いますと、ビームの 進行方向が逆になってしまいます。Munroソフトを使い始めたばかりのころはこのように、 細かい点で、TEMではレンズの向きを逆にして計算しなければならないといったような 正しい使い方をすることが出来ないでおりました。 実線と破線を比べてみますと、左端から1/4程度右に行ったところで、実測した破線は なめらかな変化をしておりますが、計算値の実線は小さなピークを作っています。これは 対物レンズの孔がここから大きくなっている位置で、メッシュの数がギャップの付近では 多くとってあるのに対し、この辺ではメッシュ数が減少しているために、正確な計算が 出来ずに漏れ磁場が突然の変化をしています。もちろん、実測の方も、ホール素子が 有限の大きさを持っているため、本当は突然の変化をしているのに、それを平均化して 示している可能性もありますので、実測値からずれているからと言って計算値の方が おかしいとも必ずしもいうことはできません。もっとメッシュ数を増やして計算を してみることだけがその解決を与えてくれるわけですが、それは当時としては出来な かったわけです。いずれにしても、商売としては、計算値が実測値よりも少しだけ 悪い大きな値を示していることが安心なわけです。 図7は、図6で収差を計算するのに使った計算と実測の軸上磁場分布をレンズの励磁 アンペアターンを変えて示しています。レンズの穴の中からの漏れ磁場の穴の直径が 変化するあたりから出る漏れ磁場のがくんとした変化は磁場が強くなるほど激しくなって いることが見て取れます。この時使っていた汎用大型コンピューターの能力ではまだ、 本当にこのレンズを正しく計算することはできない水準のものだったことが分かります。 それでも、計算で大体のことはわかるということは偉大なことだったわけで、1980年代 に可能となったコンピューターシミュレーションは大きな働きをしてくれたわけです。 チェコ・BrnoのDr. LencovaのAMAGソフトMunroソフトをベースとして、同じパラメータを使いながら、いくつかの点で改良が 加えられました。チェコの第2の都市Brnoには、科学機器の研究所があり、そこの Dr. LencovaはMunroソフトを見習って、同じパラメータを使って、独自のソフトウェア を開発しました。その特徴は、 1. メッシュ分割の自動化。Log方式のメッシュ間隔増加(図8)。 2. ATの暫増による磁気飽和の段階的考慮。 3. ICCG法によるメモリーの節約と計算時間の短縮。 チェコが共産圏にあった時代、AMAGは英国・アストン大学のProf. Mulveyの学生によって、 コメントがチェコ語から英語に翻訳され、無償配布されました。Mulveyはイギリスの会社で 電子顕微鏡の技術者でしたがその会社が電子顕微鏡から撤退すると、アストン大学の教授 となりましたが、共産圏諸国の研究者に対する援助を行っていました。自身が各国を訪問 して指導することの他、イギリスにこれらの国の技術者を呼び寄せて援助をしていました。 Lencovaののソフトの中でとりわけ重要な進歩は、ICCG法の導入によりコンピューターの サイズを小さくすることが出来たことと、計算時間の短縮が図れたことでありました。 この手法の適用によって、汎用コンピューターやミニコンピューターからパソコンの使用 による計算とグラフ表示への道が開かれました。メッシュ間隔の突然の大幅な変化は誤差の 原因となりますので、メッシュ間隔が磁石のギャップで一番小さくなり、そこから離れるに つれて少しずつ大きくなるのが最も望ましいわけで、それを実現するために、Logarismic に増大する方法が採用されました。この方法は、Munroの後でDr. Smithの研究室でミニコン 用のソフトとして開発されたソフトに採用されていた方法でしたが、それを真似した手法 でした。 Munroソフトでは、有限要素計算は、与えられた励磁ATの下でその都度計算されており、 ひとつのレンズについていろいろな励磁の強さを計算する場合に、それぞれの励磁強度 で独立に計算されていました。励磁の強さが大きい場合には、ポールピースやヨークが 磁気飽和をしますが飽和の考慮はニュートン・ラフソン法と言う繰り返し計算によって 行われます。これは、まず飽和がないとして計算をします。すると、材料の透磁率が 高いために強い磁場が出ます。ヨークなどは強い磁束密度まで磁化されます。こうしますと、 その材料は高い磁束密度に磁化されますから、透磁率が急速に小さくなってしまいます。 二度目の計算では、この弱くなった透磁率で磁場を作りますので、一回目の計算の時に比べて 弱い磁場しか発生できなくなります。第3回目の計算では、弱い磁場しか発生しなかった材料 は、今度は大きな透磁率を持ちますので、高い磁束密度まで磁化できることになります。 こうして、大きなアンペアターンの場合には、材料の透磁率が高くなったり低くなったりを 繰り返し、一定値に近づいていきます。従って、低いアンペアターンの時に いったん計算を終わらせ、その値をそれより少しだけ強いアンペアターンの場合の初期値 として使うことによって、強いアンペアターンの場合にも2~3回の繰り返しで値を収束 させることが出来ます。このように、弱いアンペアターンの場合から出発して高いアンペア・ ターンの場合に徐々に近づけていく方法で計算すれば、非常に高いアンペアターンの場合 でも少ない繰り返し数で収束させることが出来ますので、これは優れた方法です。しかしながら、 Dr. Munroのソフトウェアではこの方法が採用されておらず、磁気飽和のきつい条件の 場合になかなか飽和してくれない場合が出てきます。 ICCG法に関しては、Munroソフトでもさっそく取り入れられていますので、今では有限 要素法による磁場・電場計算はパソコンで行うのが当たり前になっています。逆に、 Munroソフトに採用されていながら、Lencovaソフトでは必要なしとして無視されている 事柄に二次の有限要素法があります。Munroソフトでは、二次の有限要素法が採用され、 曲面が自由に作れることと、メッシュの作り方が不適切で、一次の有限要素法で計算 した場合にはおかしな結果になるようなメッシュであっても、正しい結果が得られます ので、上で説明したようなLogarithmicなメッシュ間隔増加などの込み入った工夫は不要で 適当にメッシュ間隔の変化をさせても正しい解を得ることが出来ます。なぜ、Lencova ソフトで、二次の有限要素法を取り入れる必要がないと判断したのかその理由はわかり ませんが、お互いに真似はしていませんと言うことを強調するあまり、不便を利用者に 強いているだけのような気がします。 図9は、徐々に増やすアンペアターンでの計算結果で作った磁場分布を使って、球面 収差係数Cs, 色収差係数Cc、試料位置Zoを求めた例を示します。また、図10には、 アンペアターンを増やしていくにつれてヨークの根元(図の左側)で漏洩磁場が増えて 行く様子を示しています。 ところで、有限要素法は、図11にマトリックスの一部分の数値を表にして示しました ように、マトリックスの大部分の領域がゼロで、対角線方向に少しだけ数値の入って いるマトリックスを使いますので、大きなメモリーが必要になり、計算時間も長く なります。ICCG法は図10の上の表に示したように、これを数値の入っている領域だけ のマトリックスにしてしまいます。こうすると、そのままでは当然間違った答えが 出てくるだけですが、それが正しい答えに近づくまで、繰り返し計算を行うのがICCG法の やり方です。最近は、このように、間違ったデーターから出発したり、あるいは不足する データーから出発して、正しい答えに収束させる方法がいろいろ使われていますがICCG法も その一つだと言えましょう。この方法の採用によって、レンズ計算はパソコンでできるように なりました。 図12は、レンズを含む空間の有限要素マトリックスの端の処理法によって軸上磁場分布が どのように変化するかの例を示したものです。この違いを生じないようにどのように計算 領域の端を処理したらよいのかの一般的手法はまだ解決していません。それぞれの場合に ついて、同じ領域が繰り返し現れるような場合と計算領域の端が絶対的に磁場ゼロつまり、 完全反磁性の物質で仕切られている空間とみなすことが出来るような境界にあるのかの どちらの条件で近似すれば実際の場合に近くなるかを考えて、計算領域の端、境界条件を 決めなければなりません。使用するコンピューターのメモリーに余裕のある場合は、計算 するレンズの出来るだけ遠くに計算領域の端を設定すればより実験に近い条件で計算が出来 ることになります。と言うのも、実際の装置は、地球の広い空間の中に投げ出されている のであって、完全反磁性体の中に入れられているわけでもなく、同じ形のレンズが繰り返 し現れて来るわけでもありません。しかし、有限要素法での計算は、この二つの条件の どちらかを選択をしなければならないのです。このように大きな違いが計算のはじめ と終わりの領域に生じてしまいますので、なるべくレンズのぎりぎりから計算するの ではなく、レンズの外側に長い空間を取って計算すればレンズの外側近辺は正しい解に 近い答えが得られることになります。有限要素法は、その名の通り、有限の領域を切り 出して計算するのですが、計算される物質は有限の領域に閉じ込められているわけでは なく、無限の空間に置かれているわけです。この違いは有限要素法を使う限り完全には 克服できない事柄なのです。 |
|